Теплопроводность и вязкость газов
Теплопроводность и вязкость газов
Вследствие беспорядочного движения молекул газа происходит непрерывная передача механической силы, тепла и массы от одной точки пространства к другой. Эти явления переноса, называемые соответственно вязкостью (внутренним трением), теплопроводностью и диффузией, физически подобны и описываются сходными уравнениями.
Рассмотрим наиболее близкие по характеру явления — вязкость и теплопроводность.
Физическая сущность вязкости может быть объяснена, пользуясь гипотезой Ньютона, по которой предполагается, что внутреннее трение — это тангенциальная сила, пропорциональная градиенту скорости потока газа, которая зависит от его природы.
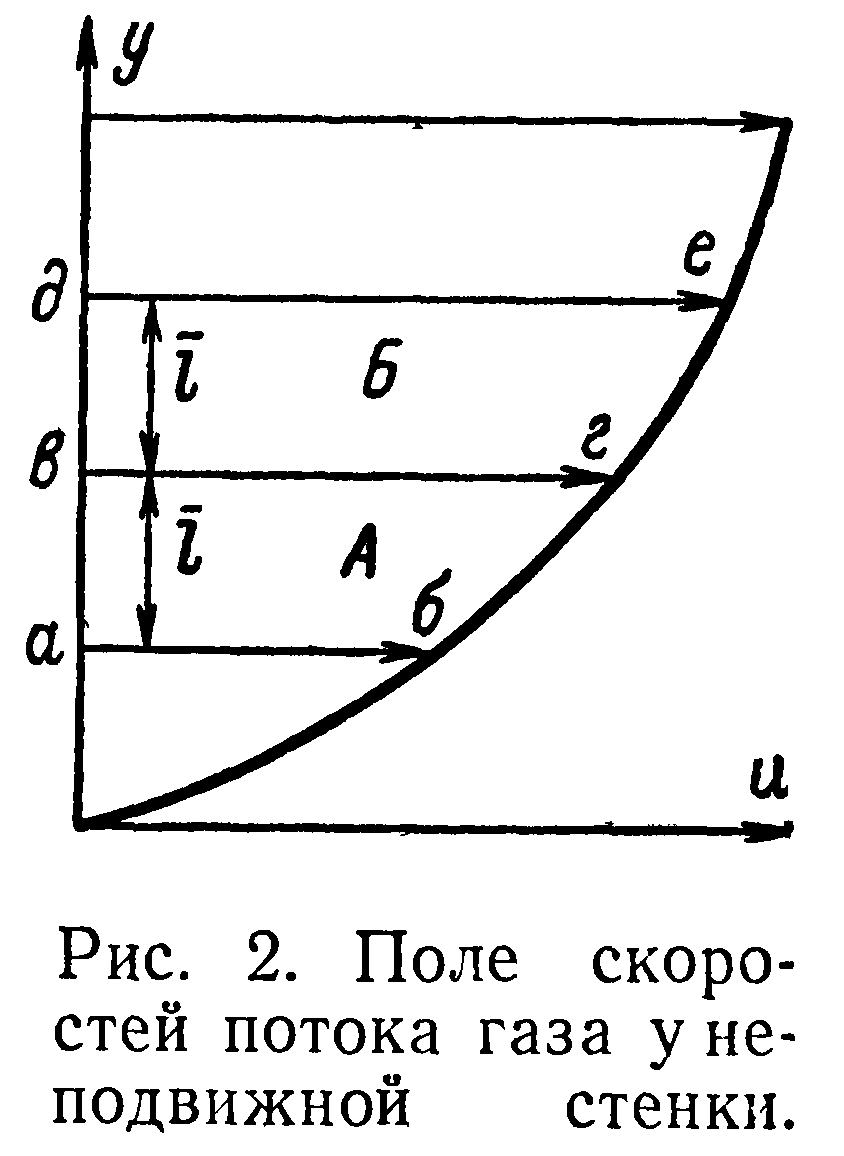
Предположим, что поток газа движется относительно неподвижной стенки (рис. 2) в направлении, совпадающем с осью скорости и. Принимается также, что вследствие взаимодействия частиц потока с твердой стенкой скорость потока у стенки равна нулю, а по мере удаления от нее скорость увеличивается по некоторому закону. Тогда сила внутреннего трения между бесконечно малыми слоями потока, параллельными неподвижной стенке, определится выражением:

или при движении одной пластины относительно другой и линейной зависимости скорости и от координаты у.
Представим себе далее, что газ разделен на слои, параллельные твердой стенке (рис. 2), а их толщина конечна и_ равна длине свободного пробега I, Тогда вследствие относительного движения смежных слоев, например А и Б, будет происходить обмен количеством движения между ними. При этом через контрольную плоскость вг молекулы из быстро движущегося слоя Б будут передавать в медленно движущийся слой Л большее количество движения, чем в обратном направлении.
Пусть m(u + vm) — количество движения любой молекулы в направлении, параллельном плоскости вг, находящейся в слое А и достигающей этой плоскости; и— скорость потока в смежной контрольной плоскости аб. Количество движения в этом же направлении любой молекулы, находящейся в слое Б и достигающей:

Если исходить из предположения, что скорости молекул равновероятны во всех направлениях, то число молекул, пересекающих единицу площади за единицу времени в любом направлении внутри газа, находящегося в покое, будет равно Для небольших скоростей потока плотность газа можно принять неизменяющейся от слоя к слою.


Поэтому действительная сила трения между слоями, выраженная как разность количества движения всех молекул, запишется формулой.
Последнее уравнение выведено в предположении, что все молекулы имеют одинаковые скорости ит и длину свободного пробега Z. С учетом действительного распределения скорости молекул газа получено более точное выражение:
Нетрудно убедиться, что произведение pZ=const справедливо в широком диапазоне изменения давления. Отсюда следует, что для любого газа вязкость не зависит от давления и должна увеличиваться с ростом температуры в соответствии с увеличением скорости по формуле (14).
Однако при низких давлениях экспериментальные значения тангенциальной силы F оказываются меньше вычисленных по формуле (42), что эквивалентно увеличению расстояния между пластинами d и физически соответствует скольжению молекул газа по твердой стенке. Поэтому формулу (42) можно записать в виде:
Сопоставляя (41) и (43), получим:

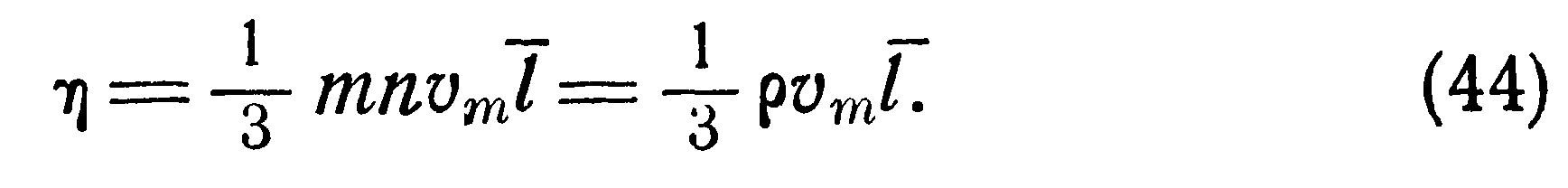



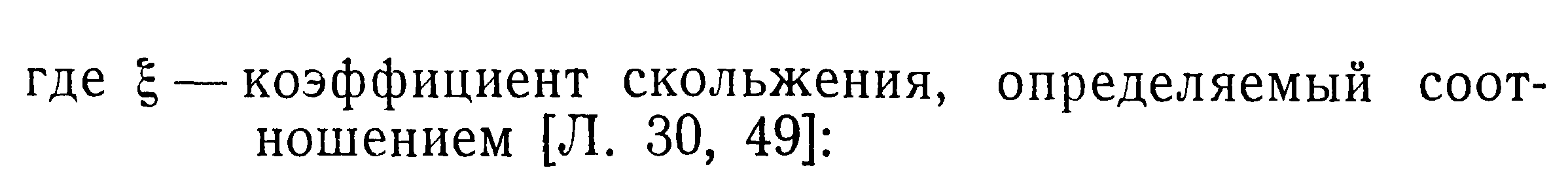

здесь f—коэффициент обмена импульсом, характеризующий относительное число молекул, отраженных от твердой стенки диффузно, к числу молекул, отраженных от стенки зеркально.
Аналогичные соотношения могут быть получены и для теплопроводности газов, так как с точки зрения кинетической теории безразлично: переносят ли молекулы от одного слоя к другому количество движения или кинетическую энергию.
Если представить, что слои А и В (рис. 2) находятся между двумя пластинами аб и де на расстоянии d=2l и их температуры соответственно равны и Т2, то градиент температуры в линейном приближении будет равен 2(Т2—Л) l/d. Учитывая последнее, находим количество переносимого через единицу поверхности тепла.
Отсюда коэффициент теплопроводности запишется:
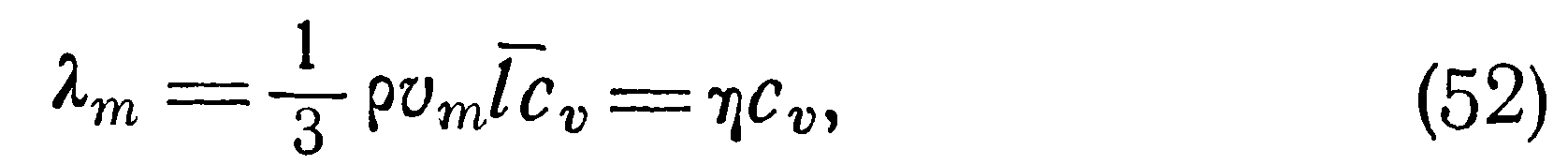

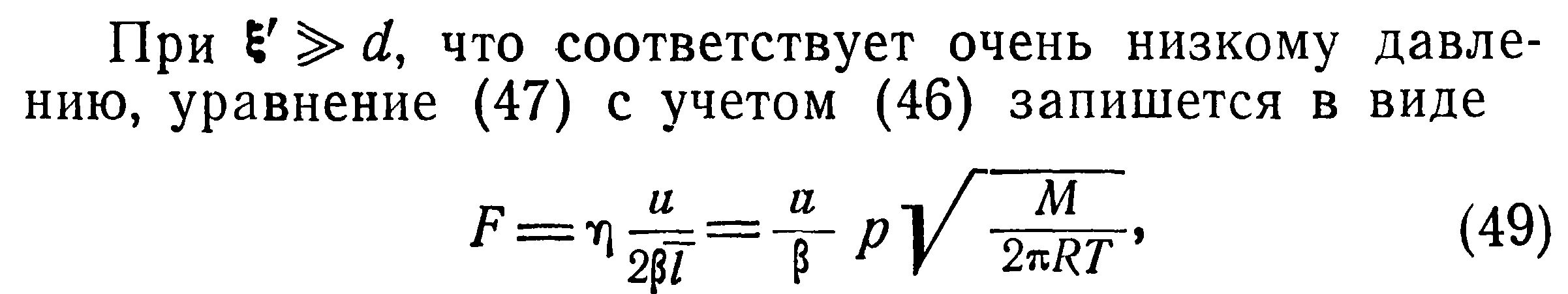



т. е. перенос количества движения от одной движущейся поверхности к другой будет прямо пропорционален давлению и скорости движущейся поверхности.
Зависимость вязкости от температуры выражается уравнением Сезерленда:
Более строгий вывод приводит к соотношению
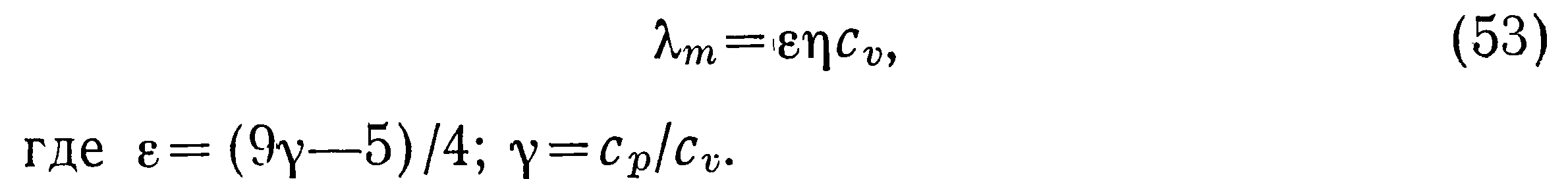

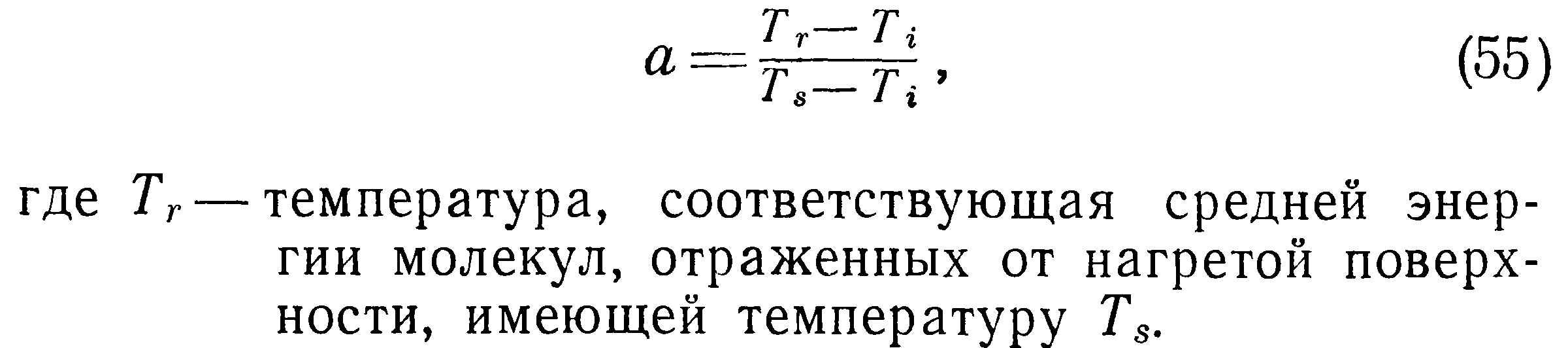
Таким образом, окончательная формула для количества переносимого тепла с площади S может быть записана:
Сравнение формул (44) и (51) указывает на полную аналогию явлений вязкости и теплопроводности. При очень низких давлениях, точно так же, как и в случае переноса количества движения, наблюдается уменьшение передаваемого тепла через слой газа.
Теория теплопроводности при низких давлениях разрабатывалась в двух направлениях, Первое направление, предложенное Кнудсеном, исходит из рассмотрения механизма переноса энергии отдельными молекулами. Второе, предложенное Смолуховским, основывается на представлении о скачке температуры в потоке газа на границе с твердой поверхностью.
С точки зрения Кнудсена молекулы газа, находящиеся первоначально при температуре Л, сталкиваясь с поверхностью стенки, температура которой равна Ts, не сразу приобретают энергию стенки. Исходя из этих соображений, Кнудсен ввел параметр, называемый термическим коэффициентом аккомодации а.
Величина коэффициента аккомодации а зависит от природы молекул твердой стенки и газа, их температуры, степени обработки поверхности и ряда других факторов. До настоящего времени экспериментальных данных по коэффициенту аккомодации для различных газов и поверхностей еще далеко недостаточно. Наиболее полные сведения по этому вопросу имеются в работах, из которых следует, чтд величина а кд" леблеТся в пределах 0,1—0,99.
На основе представлений о неполном обмене энергий молекул газа и стенки при их столкновении, Кнудсен получил соотношение для расчета переноса тепла от нагретой поверхности (площадью равной единице) к холодной, которое можно представить в следующем виде (Л. 161:
Смолуховский, изучая теплопроводность газов при низких давлениях, пришел к подобным соотношениям. Кажущееся уменьшение теплопроводности он объяснил введением понятия температурного скачка. Этот эффект количественно эквивалентен увеличению расстояния между теплообменивающимися поверхностями и физически соответствует разрыву градиента температуры у стенки. Следовательно, уравнение (54), выражающее перенос тепла между двумя параллельными пластинами, для газов при низких давлениях может быть переписано в виде:

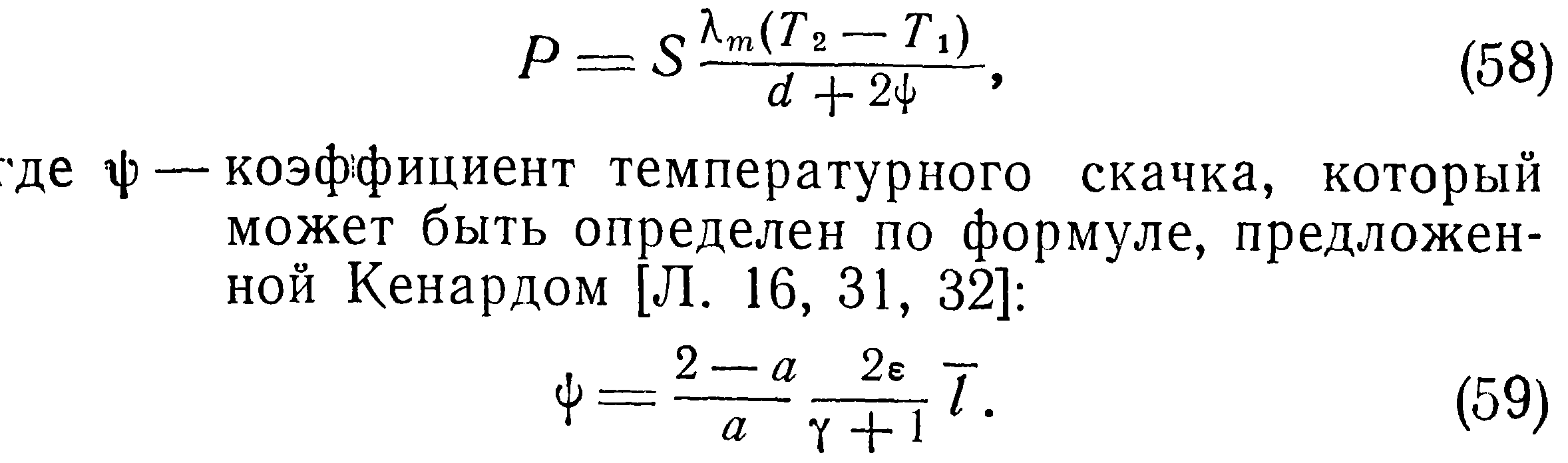
На основе рассмотрения физики взаимодействия разреженного газа со стенкой А. А. Померанцевым уточнены граничные условия и получено более обоснованное выражение для коэффициента температурного скачка.
Зависимость теплопроводности газов от температуры в первом приближении может характеризоваться, так же как и для вязкости, уравнением Сезерленда. Кроме того, по сравнению с вязкостью теплопроводность проявляет зависимость от температуры более высокого порядка через температурную зависимость теплоемкости газа cv.

