Перенос тепла в газах

Процессы теплообмена в капельных жидкостях и газах осуществляются конвекцией, теплопроводностью и лучеиспусканием. Конвекция, представляющая собой процесс переноса тепла за счет макроскопического перемешивания отдельных порций газа, по своему действию и физической сущности не отличается от теплопроводности. Поэтому в практике под конвекционным теплообменом понимают совокупное действие конвекции и теплопроводности.

Конвекционный теплообмен зависит от природы возникновения и режима движения, рода и физических свойств жидкости, формы и размеров поверхности твердого тела и ряда других факторов. Движение жидкости, обусловленное разностью плотностей нагретых и холодных объемов, называется свободным, а происходящий при этом перенос тепла — естественной конвекцией. Связь между количеством тепла Р, переданного при свободном движении жидкости, и условиями теплообмена устанавливается формулой Ньютона:

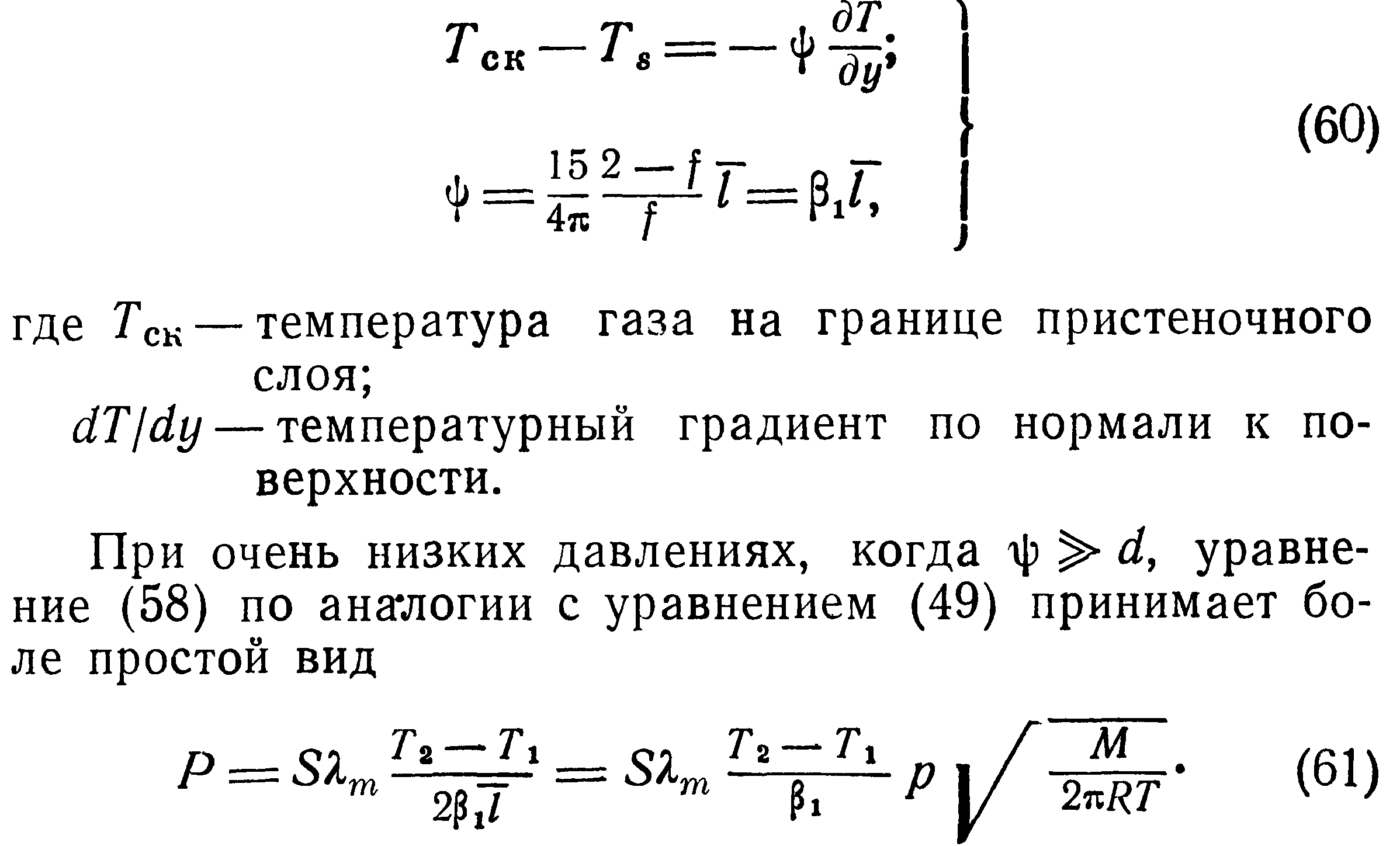
Применение формулы Ньютона принципиальных упрощений не дает, так как вся сложность процесса теплообмена переносится на определение коэффициента теплообмена а_к, который является функцией многих параметров. Однако, как показали многочисленные исследования, решающее влияние на процесс свободной конвекции оказывают физические свойства среды и температурный напор.

Существенную роль при изучении процессов теплообмена играет теория подобия, в соответствии с которой устанавливается связь не между отдельными физическими величинами, характеризующими процессы переноса тепла, а между составленными из этих величин безразмерными комплексами — критериями. Это позволяет систематизировать экспериментальные данные теплообмена и получать обобщенные критериальные уравнения.

Для условий теплообмена естественной конвекцией, при которых работают датчики большинства теплоэлектрических приборов, критериальные уравнения имеют вид:

Значения коэффициентов С, п, т определяются экспериментально и в общем случае являются функциями произведения GrPr как аргумента.

Влияние формы и размеров образцов на процесс теплообмена со средой в общем случае не являются определяющими факторами, что математически выражается равенством нулю показателя степени т в уравнении (63). Влияние формы обычно учитывается подходящим выбором определяющего размера системы. Однако, в некоторых частных случаях, и в особенности при теплообмене в разреженном газе, влияние формфактора становится значительным, а при определенных условиях решающим. Классическими формами теплообмениваю-щнхся образцов являются: пластина, цилиндр и шар. К ним можно свести практически все встречающиеся другие формы.

Если образец расположен в пространстве, ограниченном стенками, то условия движения среды будут зависеть как от формы и геометрических размеров пространства, так и от рода жидкости и интенсивности процесса теплообмена. При очень малых значениях аргумента (GrPr<10³) теплообмен в ограниченном пространстве будет определяться чистой теплопроводностью . В простейшем случае, например, для двух коаксиальных цилиндров бесконечной длины, независимо от их ориентации, критерий Nu для теплопроводности будет:

Ленгмюр, изучая теплообмен тонких проволок, высказал предположение, что потеря тепла происходит через пленку прилегающего к проволоке газа, внешняя поверхность которой находится на расстоянии D/2 от оси проволоки. Ленгмюр показал,что величина/) удовлетворяет соотношениям.

Экспериментально было показано, что для воздуха при атмосферном давлении и температуре 293,2° К величина В = 0,43 и очень слабо зависит от температуры.

Воспользовавшись идеей Ленгмюра о неподвижном цилиндрическом слое газа вокруг нагретой проволоки, через который перенос тепла происходит теплопроводностью, Герман решил для этого случая уравнение пограничного слоя. Критериальная зависимость, полученная Германом аналитически для горизонтальной проволоки.

Величина числителя второго слагаемого в правой части уравнения (67) получена приближенно, основываясь на том допущении, что толщина пограничного слоя вокруг проволоки незначительна по сравнению с диаметром самой проволоки. Последнее не соответствует действительности для тонких проволок и противоречит идее теплопроводного слоя.

Для разрешения этого противоречия можно воспользоваться соотношением (65) и вычислить новое значение коэффициента в уравнении (67), полагая Nu = 0,5 при GrPr=l-10^-3.

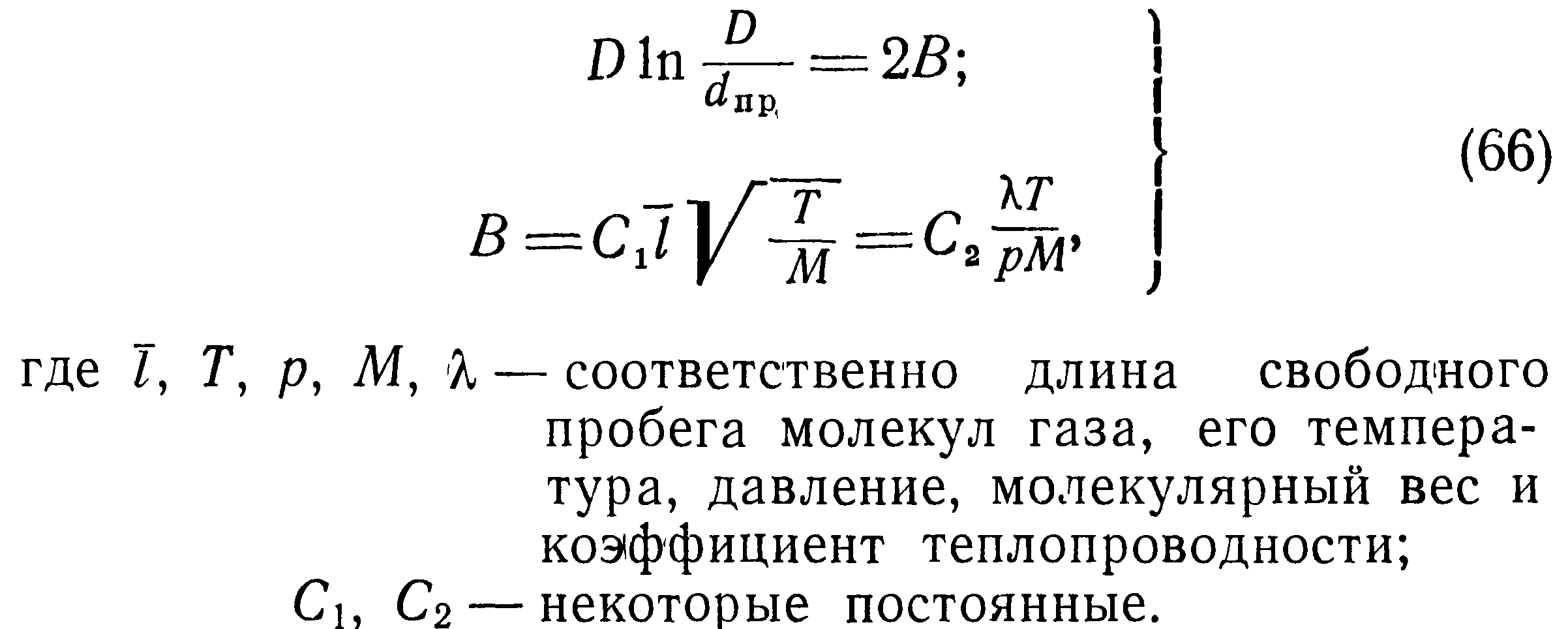
При этом необходимо предварительно придать формуле (67) общепринятый вид, введя в нее критерий Прандтля, равный для воздуха 0,714.

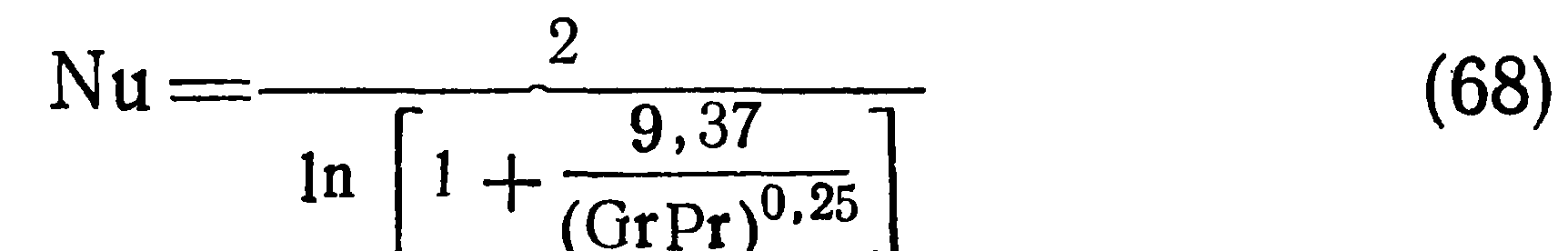
Полученное таким образом уравнение будет справедливо для теплообмена в вязком потоке при значении аргумента GrPr> 10-³. Верхняя граница применимости формулы (68) подлежит экспериментальной проверке.

Для вывода более общих уравнений теплообмена в вакууме Кайт, Мэдден и Пайрет провели экспериментальные измерения потерь тепла от сфер и цилиндров в газ (воздух, гелий и аргон) в диапазоне давлений от 13,3 до 10⁵ нм² и диапазоне температур от 283,2 до 438° К. При обработке экспериментальных данных авторы {Л. 55] сделали два отступления от классической практики: а) за характерный размер исследуемого образца приняли его диаметр _плюс удвоенную длину свободного пробега — d=d+2l б) ввели понятие теплопроводной пленки толщиной 0,5 (Ь—d¹), имеющей такое же сопротивление тепловому потоку как и пленка конвекционного пограничного слоя, толщина которого 0,5 (D—d). Здесь D, Ь — внешний диаметр пограничного слоя вокруг цилиндрического или сферического образца и соответствующий диаметр образца с эквивалентной пленкой. Полученные в результате такой обработки критериальные уравнения, выражающие потери тепла Р от образцов, могут быть записаны в следующей форме:

для сфер:

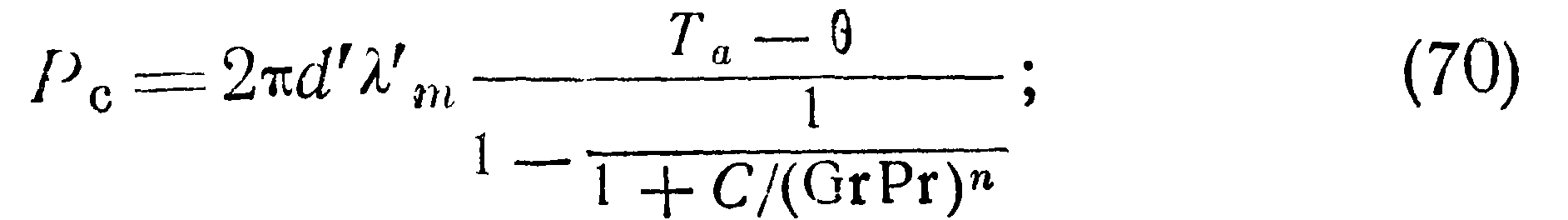
для горизонтальных цилиндров:

для вертикальных цилиндров:

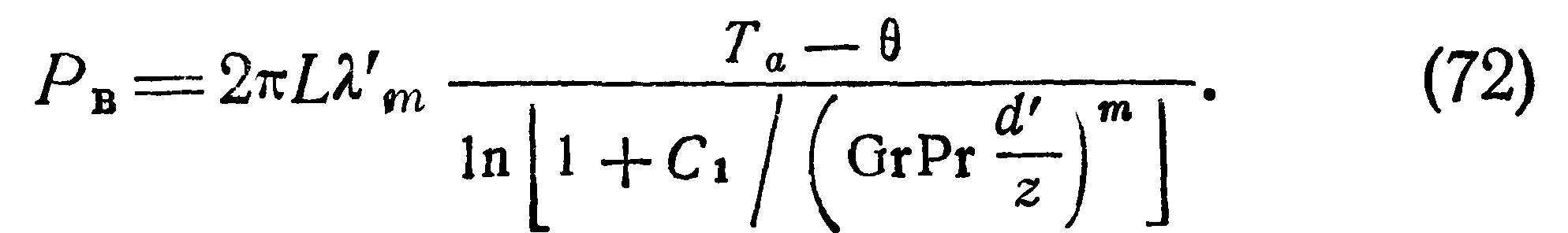
За определяющую температуру принята Т_т=, —С,5(Т_а+ 6). Значения температуры Т_а определяются из уравнения Кнудсена (56). При этом критерием правильности расчета температуры является равенство вычисленной потери тепла по формуле (56) и по одной из формул (70) и (72). Когда же давление газа таково, что длина свободного пробега молекул мала (/—О) и эффект снижения потерь тепла вследствие увеличения определяющего размера становится незначительным, то за определяющий размер в формулах (70) — (72) можно принять диаметр d, а за определяющую температуру T_m—0,5(T_s+ в). Во всех вышеуказанных случаях измерение температуры среды 0 необходимо производить за пределами пограничного слоя.

Для расчета теплообмена при очень низких давлениях, когда толщина пограничного слоя настолько велика, что температура, измеренная вдали образца, попадает в зону пограничного слоя, авторы {Л. 57] рекомендуют следующие формулы:

для сфер

для цилиндров

Приведенные выше формулы по данным их авторов дают хорошее совпадение с экспериментом. Вместе с тем сравнительно небольшой диапазон охваченного давления далеко не исчерпывает поставленной задачи, а полученные формулы имеют два существенных недостатка для области молекулярно-вязкостного режима.

Во-первых, температура Т_а определяется из условия равенства потерь тепла свободно-молекулярным потоком в пристеночном слое толщиной I и потерь путем конвекции за его пределами — в пограничном слое. Задача определения температуры Т_а становится, таким образом, неопределенной и ее решение возможно лишь методом последовательных приближений.

Во-вторых, выбор определяющего размера d4-2Z может быть оправдан лишь для малых чисел Кп и неприемлем для больших вследствие проявления эффекта кривизны на поверхности тел вращения.

Кроме того, эти формулы слишком громоздки и поэтому ограниченно пригодны для разработки и анализа работы датчиков приборов, чувствительных к изменению давления.

Подводя итог краткой сводке проблем, возникающих при расчете конвекционного теплообмена в разреженном газе, следует заключить, что до настоящего времени менее всего изученной остается область давления, соответствующая молекулярно-вязкостному режиму при теплообмене в неограниченном пространстве.

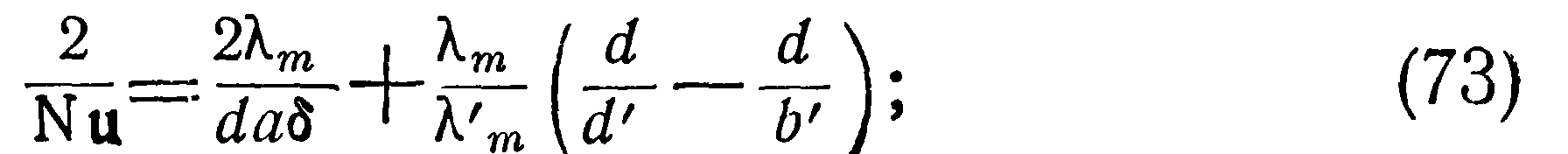
Задача эта по существу сводится к определению толщины пограничного слоя или к определению температурного поля по нормали к поверхности.

Теоретическому и экспериментальному исследованию температурного поля в пограничном слое посвящена работа А. Н. Девойно. Однако полученная в этой работе система нелинейных уравнений и численный результат может практически дать лишь с помощью электронной вычислительной машины и пригодна только для простейшего случая — вертикальной пластины. Что касается экспериментальных данных, то они хорошо согласуются с теорией и могут быть использованы для качественной оценки изменения толщины пограничного слоя с изменением давления.

Для того чтобы придать формуле (69) более универсальный характер, распространив ее применение на теплообмен в неограниченном пространстве, вместо наружного диаметра цилиндра D можно принять внешний диаметр теплопроводной пленки, вычислив ее из соотношений (66). При этом необходимо, очевидно, исходить из условия Z>_H<uD<Z>o- Здесь D_a — значение D, которое определяется для вязкого потока из условия Nu = 0,5=const при GrPr < 10^-3, когда вторым слагаемым знаменателя в уравнении (69) можно пренебречь; >о — диаметр оболочки. Для очень тонкой проволоки при GrPr <<10^-3 и атмосферном давлении может оказаться, что вследствие конечного значения числа Кп, Nu<0,5. В этом случае значение D_B определяется с учетом температурного скачка или по формулам (66).

При давлениях, когда диаметр теплопроводной пленки ограничивается оболочкой (D=D₀), уравнение (69) совпадает с уравнением Смолуховского.

Таким образом, в сочетании с уравнениями (66) уравнение (69) может количественно характеризовать процесс теплообмена цилиндрических тел при естественной конвекции в ограниченном и неограниченном пространстве. Верхний предел справедливости формулы (69) соответствует GrPr=10-³, а нижний не ограничивается. При GrPr > 10-³,* как уже отмечено выше, предпочтительнее пользоваться уравнениями (66).

Составляющая потерь тепла изучением определяется по формуле Стефана—Больцмана:

где 8 — коэффициент излучательной способности поверхности— коэффициент черноты;

Со — коэффициент лучеиспускания абсолютно черного тела. Как видно из формулы (75), потери тепла излучением не зависят от давления газа.