Методика расчета электрических цепей с терморезисторами в стационарном режиме

Основной целью расчета электрической цепи является нахождение токов и распределения падений напряжения в отдельных ее элементах. Эта задача принципиально может быть решена графически, аналитически и графоаналитически. Однако, вследствие явно выраженной нелинейности вольт-амперной характеристики терморезистора и отсутствия ее аналитического выражения в явном виде, аналитический метод расчета получил ограниченное применение.

Графический метод расчета электрических цепей, основанный на известном из анализа методе решения нелинейных уравнений, более приемлем в данном случае. Этот метод сводится к построению графиков вольт-амперных характеристик линейных и нелинейных элементов и нахождению точек их пересечения при заданных режимах. Применительно к электрическим цепям постоянного тока с нелинейными элементами, находящихся в различных комбинациях между собой и линейными элементами, этот метод подробно разработан В. Е. Вартельским.

Особенно удобным является графоаналитический метод, практические приемы которого хорошо известны из работ. Сущность метода сводится в основном к графическому решению уравнений, составленных для нелинейных элементов цепи, и аналитическим расчетам отдельных узлов, содержащих линейные элементы.

Пользуясь этими методами, можно с достаточно вы-сокой для практики точностью решать уравнения Кирхгофа по существу для любых комбинаций линейных и нелинейных элементов электрической цепи. Здесь будут рассмотрены только две простейшие и наиболее распространенные комбинации: последовательная цепь терморезистора и линейного сопротивления и мостовая схема с терморезистором в одном плече. В случае более сложных цепей методика существенно не изменяется.

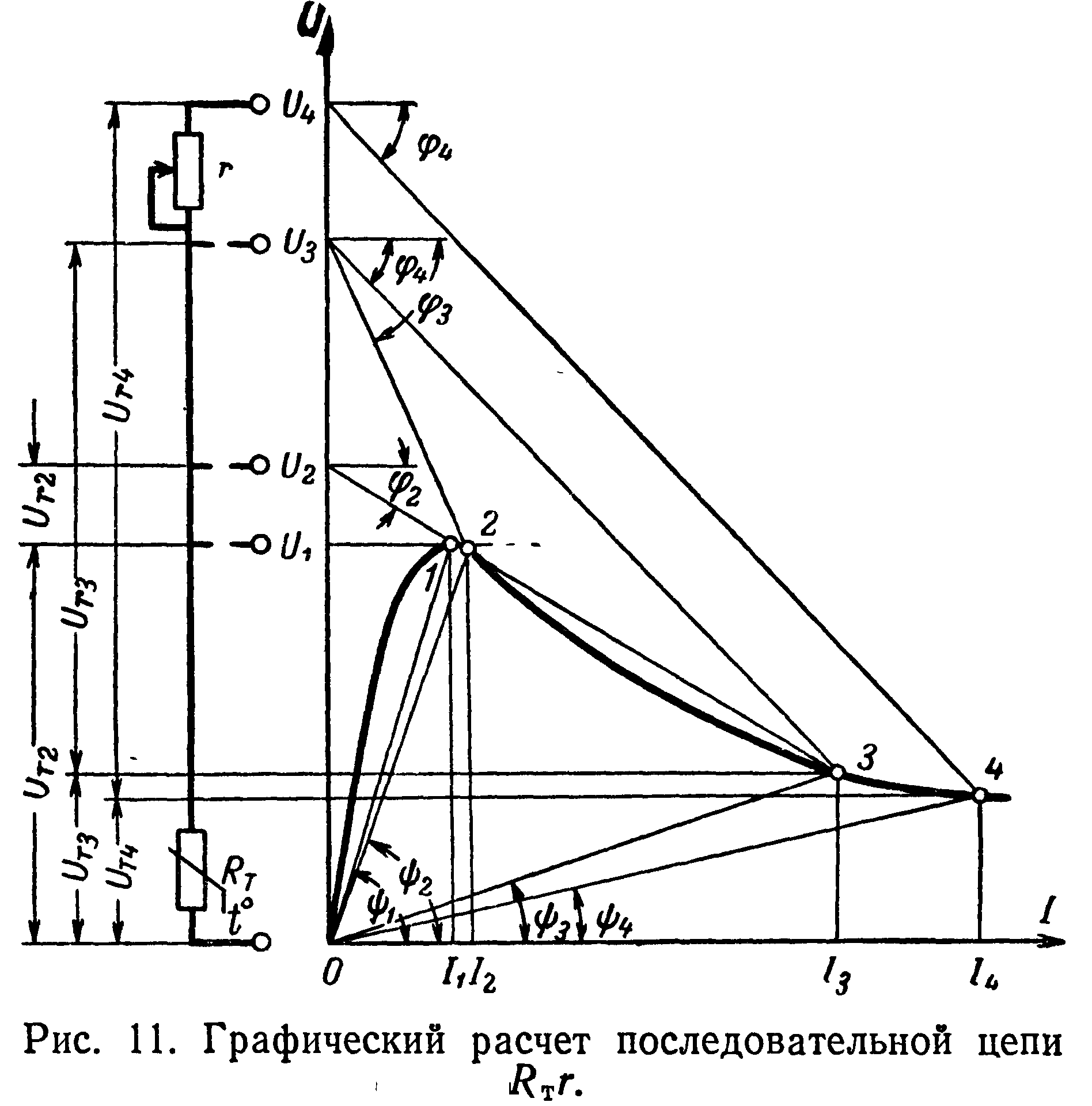
Рассмотрим последовательно цепь (рис. 11), составленную из регулируемого линейного резистора г и терморезистора 7_т, для которой будет справедливо уравнение

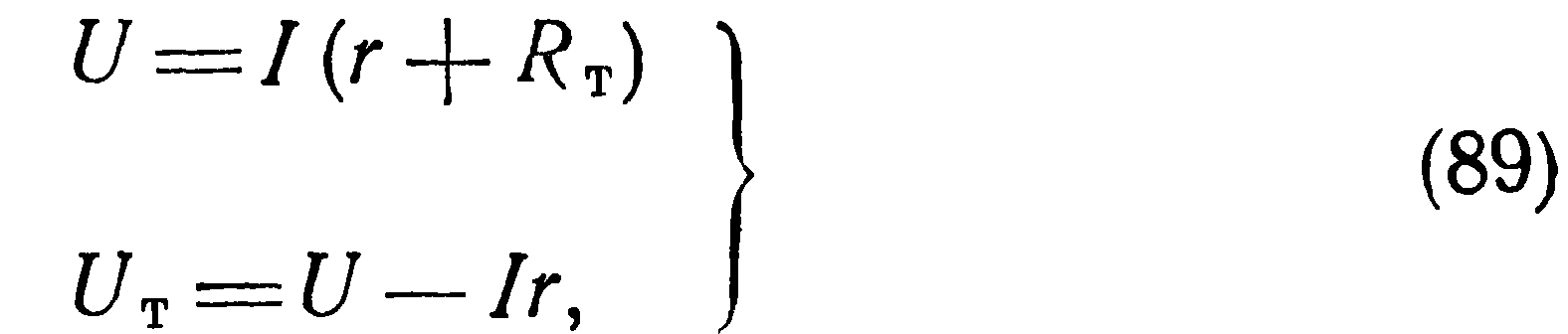
или

Выполненные на рис. 11 построения основаны на соотношениях (89), т. е. отрезки, изображающие падения напряжения, суммируются и дают падение напряжения во всей цепи, а величина тока в цепи определяется абсциссой в точке пересечения вольт-амперных характеристик обоих элементов. Последовательность расчета видна из построения. Здесь следует лишь указать на некоторые частные, но практически важные случаи расчета цепи 7_тг.

При напряжении питания цепи С7₂ (рис. 11) и сопротивлении линейного резистора /2 (угол <р*2 = arctg Г2) возможны два решения. Первое решение соответствует координатам точки 2 (неустойчивый режим), второе — координатам точки 3 (устойчивый режим). При неустойчивом режиме незначительное изменение параметров цепи (повышение питающего напряжения, уменьшение линейного сопротивления) или изменение состояния среды (повышение температуры, ухудшение условий теплообмена) равновесие нарушается и цепь стремиться к новому установившемуся состоянию, соответствующему ее параметрам в точке 5. Возвращение к исходному, но устойчивому состоянию возможно путем увеличения линейного сопротивления (например, до величины Гз) с последующим повышением питающего напряжения до значения U₃,

Как видно из построений на рис. 11, для обеспечения устойчивости цепи R_Tr необходимо выбрать ее электрические параметры такими, чтобы угол наклона вольт-амперной характеристики сопротивления линейного резистора был больше угла наклона касательной в любой точке падающего участка вольт-амперной характеристики терморезистора. Иначе говоря, необходимо, чтобы т.д, где R = dU_TdI — дифференциальное (динамическое) сопротивление терморезистора, имеющее на падающем участке вольт-амперной характеристики отрицательное значение.

Одним из наиболее часто встречающихся случаев является состояние цепи 7_тг, при котором г=0. В этом случае нормальная работа терморезистора возможна только на восходящем участке его вольт-амперной характеристики, т. е. когда напряжение питания не превышает максимума характеристики: U_x<U_m. В противном случае вследствие лавинообразного нарастания тока до недопустимо большой величины (теоретически до бесконечности) неизбежно повреждение терморезистора.

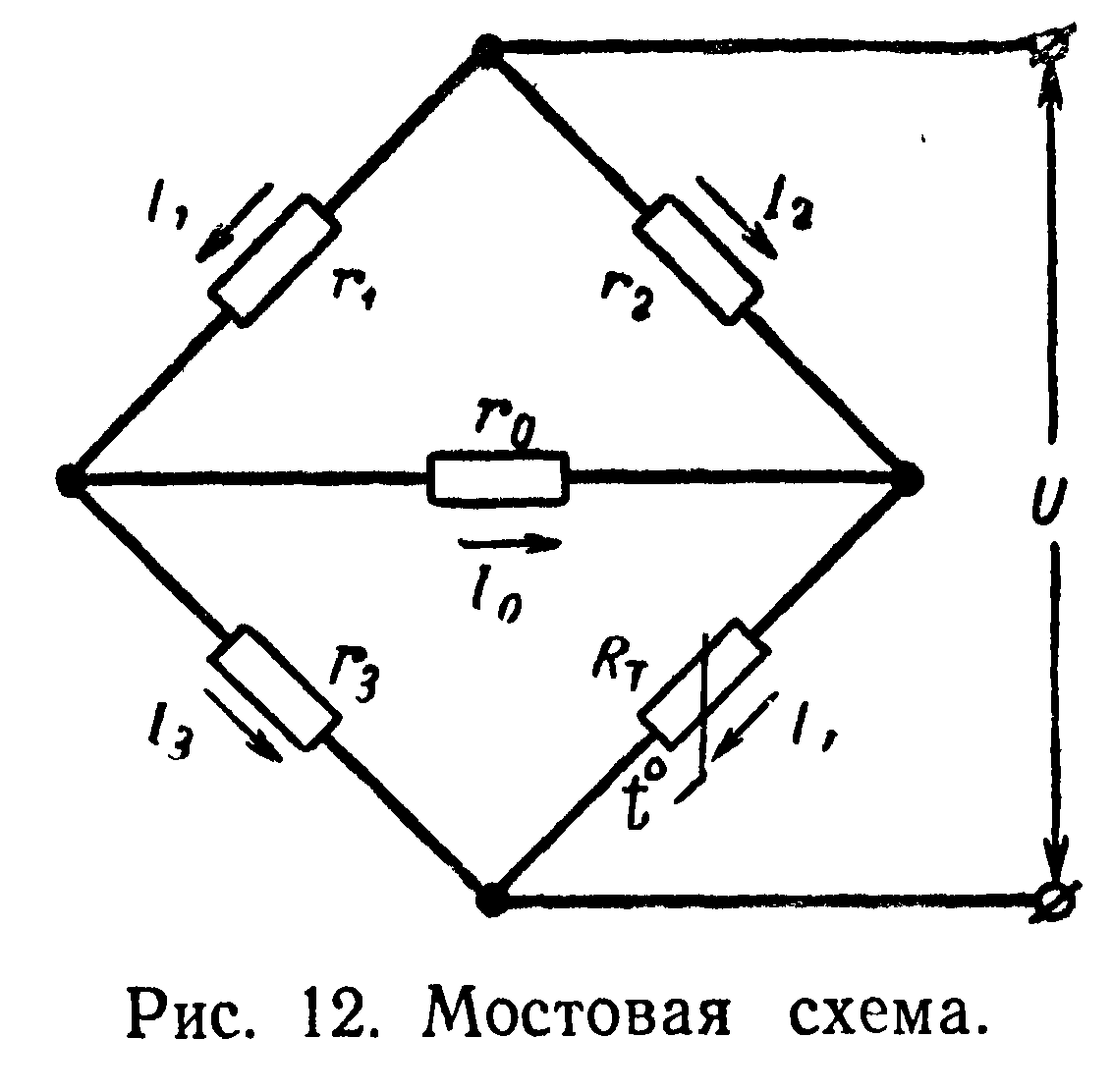
Для второй распространенной схемы — неуравновешенного моста, изображенного на рис. 12 — будут справедливы уравнения:

Как уже отмечалось, аналитически рассчитать токи и напряжения в ветвях схемы по приведенным формулам трудно вследствие отсутствия аналитического выражения 7_т через параметры электрической цепи в явном виде. При графическом расчете неуравновешенного моста, схема которого изображена на рис. 12, в зависимости от величины сопротивления выходной диагонали Го различают два возможных случая.

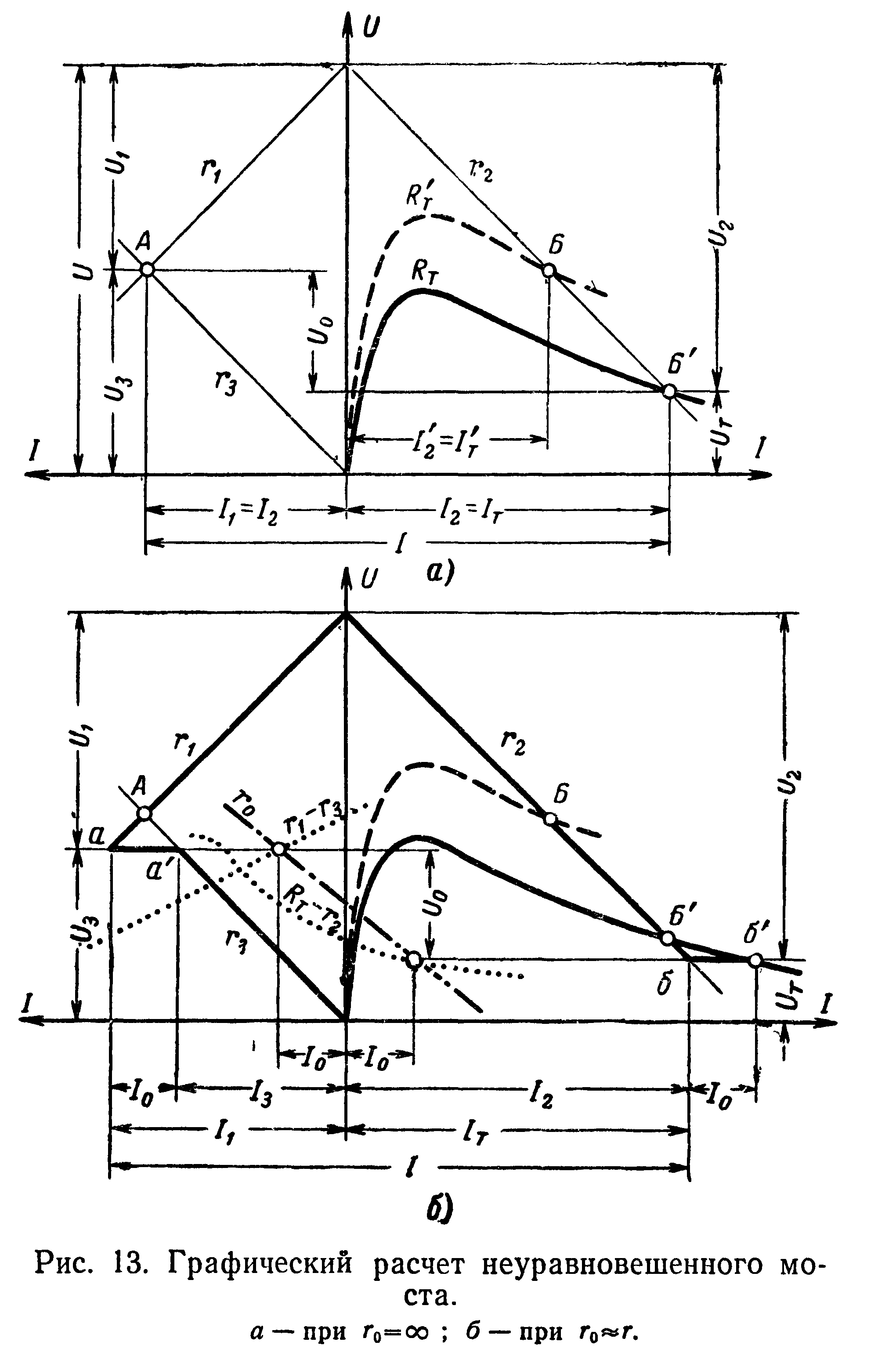
Первому случаю соответствуют построения, выполненные на рис. 13,а. При таких условиях сопротивления плеч моста ц—г₃ и г₂—Вт можно рассматривать как последовательные сопротивления, которые включены на полное напряжение, приложенное к мосту. Поэтому для каждой пары этих сопротивлений решением будут координаты точек А и Б соответственно для плеч Г1— /₃ и г₂—7_т.

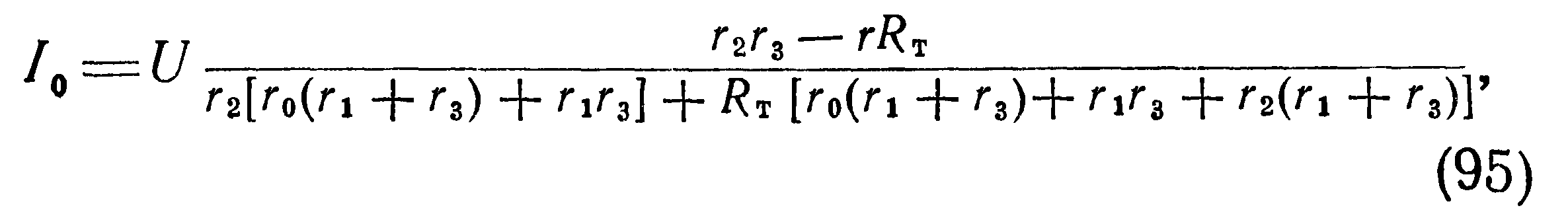
При определенных условиях термической связи с окружающей средой, соответствующих его вольт-амперной характеристике, которая показана пунктирной линией, мост будет находиться в равновесии и ординаты точек А и Б будут равны, т. е. напряжение на выходе моста равно нулю. При изменении условий теплообмена вольт-амперная характеристика терморезистора деформируется и принимает вид, изображенный сплошной линией. В этом случае значения тока и падений напряжения на сопротивлениях г% и /_т будут характеризоваться координатами точки Б, а величина напряжения U_o определится как разность ординат точек А и Б.

Для неуравновешенного равноплечего моста (п = = ^/,2=з=р; г₀=оо) напряжение U_o иногда удобно выразить через его известные параметры и мощность, рассеиваемую терморезистором (Л. 6]. Если такой мост балансируется при минимальной мощности рассеяния терморезистора, то при отклонении его от равновесия будут справедливы следующие соотношения:

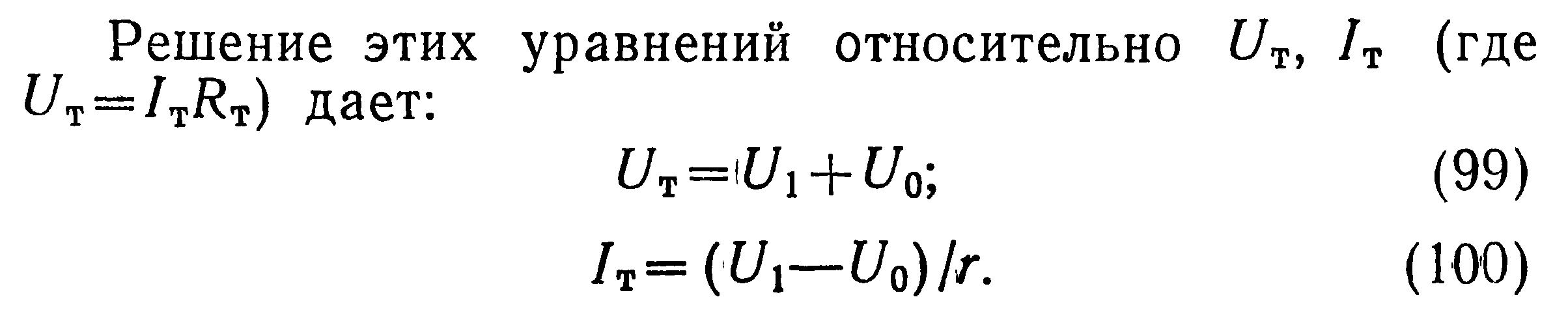
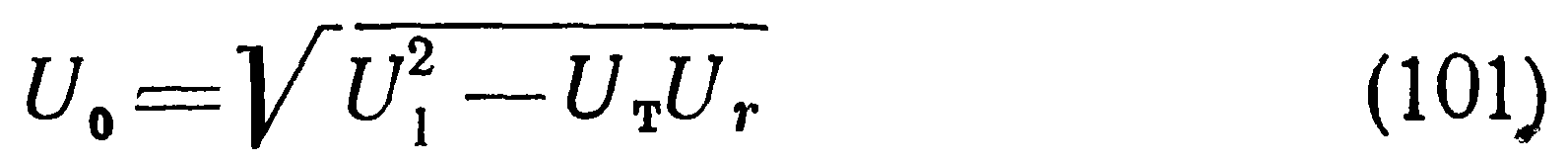
Для расчета моста, током выходной диагонали которого пренебречь нельзя, выполнено построение на рис. 13,6. При построении учитывались соотношения (90) — (94). Кроме того, принималось очевидным, что при наличии нагрузки в выходной диагонали падение напряжения в ней должно быть всегда меньше.

Построены вспомогательные кривые разности сопротивлений резисторов Г—г₃ и Я_т—г%, показанные на рис. 13,6 мелким пунктиром, и линия г₀, параллельная вольт-амперной характеристике сопротивления выходной диагонали (на рис. 13,6 показана штрихпунктиром). Если линия г₀ проведена так, что абсциссы точек пересечения с разностными кривыми равны между собой, то каждая из полученных абсцисс дает величину тока /о« а разность ординат этих же точек будет падением напряжения на выходной диагонали Uq. Дальнейшая последовательность определения токов и падений напряжения в остальных элементах видна из построений.

Из рис. 13,6 нетрудно проследить, что изменением наклона характеристики резистора г₀ можно получить различные значения токов и падения напряжения на нем. При переходе к предельному значению сопротивления Го—0 схема моста вырождается и превращается в последовательно-параллельную цепь, состоящую из резистора Г1,2 = Г11|г2 и последовательно с ним включенных резисторов г₂ и /_т. Последние два элемента между собой включены параллельно. Отыскание токов и распределения напряжений в такой цепи существенно упрощаются. Достаточно сначала графически сложить сопротивления резистора г₂ и терморезистора R_T (суммируя абсциссы их вольт-амперных характеристик) и затем рассматривать их как два последовательно включенных— линейного и нелинейного сопротивлений. Следует, однако, иметь в виду, что при некоторых комбинациях параметров мостовой схемы, устойчиво работающей при Го¥=О, уменьшение сопротивления выходной диагонали до нуля может привести к существенным качественным изменениям, а иногда и к потери устойчивости.

Другой предельный переход r_Q = oo рассмотрен выше.