Динамические параметры и характеристики терморезисторов

Как элемент электрической цепи, терморезистор характеризуется сопротивлением S_т, которое связано с его температурой соотношением (76). Температура в свою очередь является функцией состояния окружающей среды и зависит от совместно протекающих процессов поглощения или выделения тепла в терморезисторе и ее рассеяния в окружающую среду. В отличие от стационарного состояния, характеризующегося тепловым равновесием, неустановившийся (динамический) режим терморезистора характеризуется процессом изменения его температуры во времени. Динамический режим возникает обычно либо вследствие изменения состояния и свойств среды (изменение температуры, давления, тепЛопроводности, вязкости й т. д.), либо вследствие нарушения баланса между подводимой и рассеиваемой терморезистором мощности.

Кривые, изображающие изменения во времени температуры терморезистора (или параметров, функционально связанных с температурой — сопротивления, тока, напряжения), вызванные нарушением теплового равновесия, называются динамическими характеристиками терморезистора. Наибольший практический интерес представляют динамические характеристики, изображающие изменения тока во времени при скачкообразном изменении параметров электрической цепи (питающего напряжения, внешнего линейного сопротивления) или коэффициента теплообмена и сохранении температуры окружающей среды неизменной 6 = 6₀ Символически эти характеристики обозначаются:

Кроме того, динамической характеристикой принято считать ломаную линию, изображающую в координатах U—I зависимость между током /_х, протекающем по терморезистору, и падением напряжения на нем (7_т в неуста-новившемся режиме. Эта характеристика, называемая динамической вольт-амперной характеристикой, будет показана ниже на рис. 15.

Длительность неустановившегося процесса в цепи с терморезистором зависит от электрических параметров цепи и тепловой инерции терморезистора, численно характеризующейся постоянной времени т_б, которая является его основным динамическим параметром. Физический смысл параметров т₀ становится ясным после рассмотрения дифференциального уравнения свободного охлаждения терморезистора.

Предположим, что первоначально он характеризовался температурой 1 — более высокой, чем температура окружающей среды 0. Пусть с некоторого момента началось его свободное охлаждение и за время dz в окружающую среду рассеяно¹ k(T — где Т — температура терморезистора к концу отрезка времени d. Очевидно, что работа численно равна уменьшению запаса тепла в рабочем телетерморезистора на величину CdT (дж), т. е.

Из последнего уравнения видно, что охлаждение терморезистора следует экспоненциальному закону, а параметр и₀ обозначает время, в течение которого перепад температур б в процессе свободного охлаждения терморезистора уменьшается на (1—е^-1) 100=63% от своего первоначального значения бь Проводя последовательно аналогичные рассуждения для процесса нагревания терморезистора, можно придти к подобным соотношениям.

Несколько более сложными оказываются переходные процессы в терморезисторе при нагревании его электрическим током.

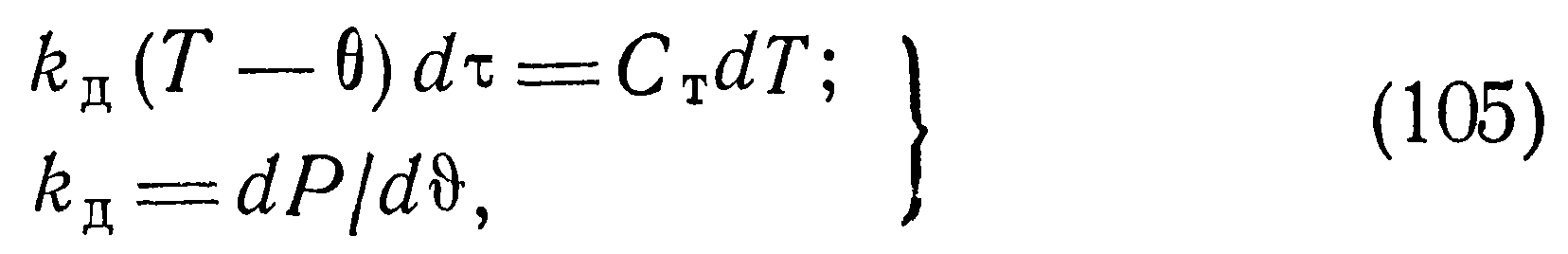
В этом случае часть мощности Р_т = из которого видно, что цепь, содержащая терморезистор, реагирует на изменение величин, входящих в правую часть уравнения. Это уравнение интегрируемо и его решение может быть доведено до численного результата, если известны параметры С_т и &_д. Первый параметр — теплоемкость С_т проявляет слабую зависимость от температуры и принимается обычно постоянным для данного типа терморезистора в его рабочем диапазоне температур. Второй — динамический коэффициент рассеяния &_д — также несколько зависит от температуры и в сильной степени зависит от условий теплообмена (состояния и свойств среды). Его определение требует снятия экспериментальной вольт-амперной характеристики.

Обычно решение уравнения (108) записывается в виде:

или

Уравнение (108) может быть переписано в несколько ином виде:

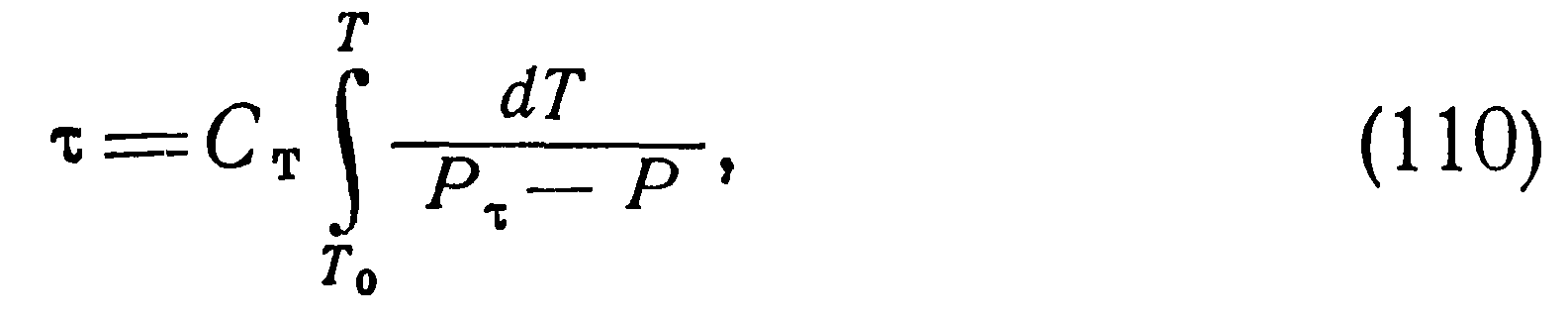
При оценке динамической погрешности прибора с терморезисторным датчиком или для анализа его устойчивости при неустановившемся режиме необходимо построение динамических характеристик. Эта задача может быть выполнена либо путем экспериментального снятия динамических характеристик, либо аналитически. В последнем случае необходимо знать динамические параметры терморезистора и уметь их определять. В тех же случаях, когда применение терморезисторов основано на использовании их инерционных свойств (реле времени, генераторы инфранизких частот, стабилизаторы напряжения и т. д.), введение в расчет динамических параметров становится принципиально необходимым.

Для определения динамических параметров терморезисторов предложен ряд методов, которые сводятся по существу к осциллографированию изменений электрических параметров терморезисторов. В одних случаях изменения этих параметров вызываются за счет влияния внешней среды, в других — за счет внутренних источников тепла, возникающих при прохождении через терморезистор электрического тока.

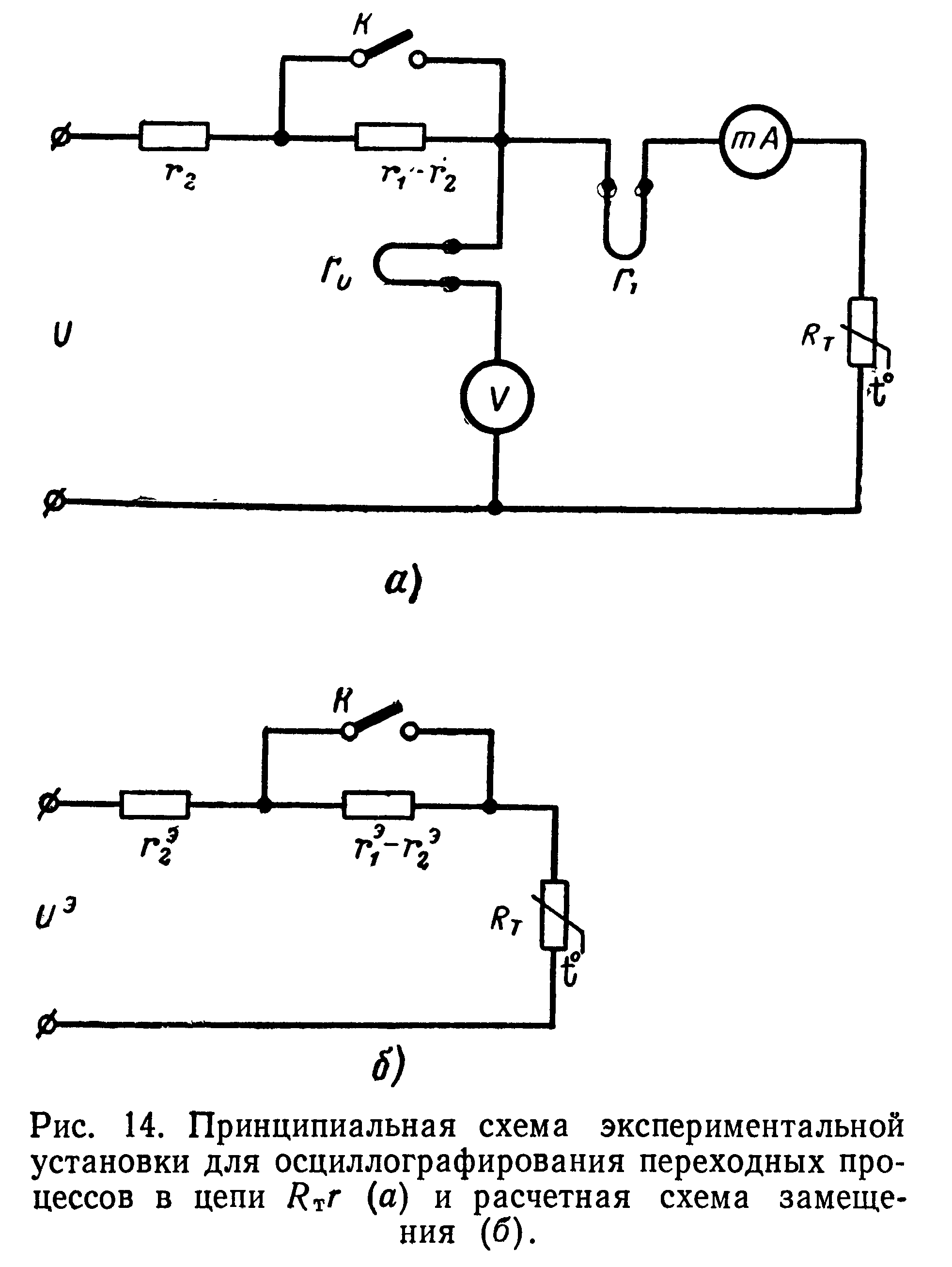
Достаточно точными и наиболее простыми в осуществлении являются методы, основанные на нарушении статической устойчивости электрической цепи путем скачкообразного изменения параметров самой цепи, например линейного сопротивления г. Ниже рассматривается один из таких методов. Схема измерений (рис. 14) позволяет регистрировать одновременно изменение во времени и тока и напряжения. На рис. 14,6 изображена схема замещения, учитывающая влияние сопротивления вольтметра г_в (сопротивлениями миллиамперметра, гальванометров осциллографа Г-1 и Г-2 можно пренебречь). Параметры эквивалентной схемы рассчитываются по формулам:

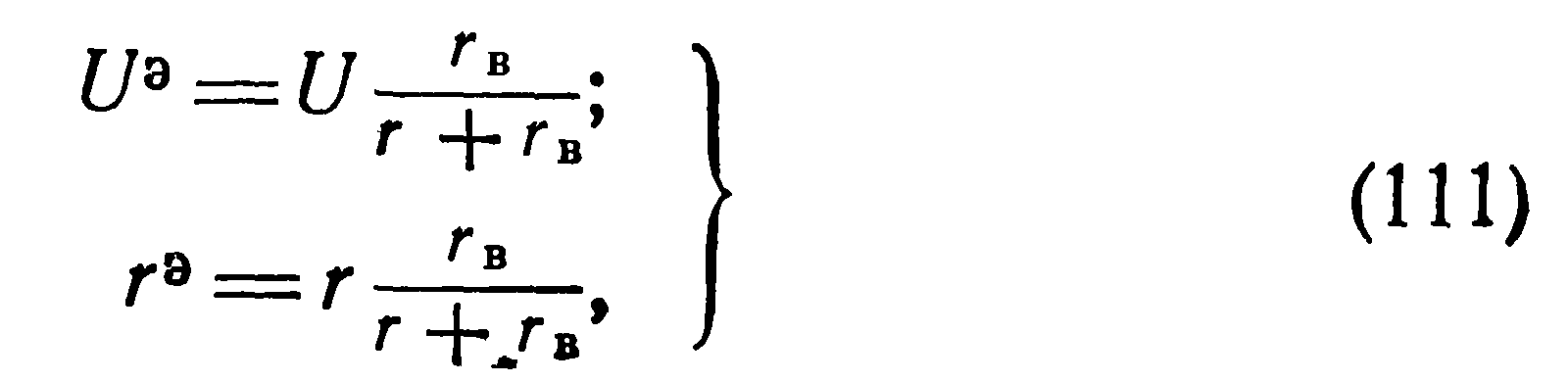
На рис. 15 схематически изображены динамические характеристики терморезистора при следующих значениях индексов: т, т— нижние индексы, указывающие соответственно на принадлежность параметра к стационарному или переходному режиму; 1, 2 — нижние индексы, указывающие отношение параметра к цепи, в которую включены резисторы Г1 и г₂ соответственно, т — верхний индекс, который указывает, что при данном значении параметра мощность, идущая на изменение теплосодержания термистора.

Если сдвигом фаз между вектором тока, протекающего через терморезистор, и вектором приложенного к нему напряжения можно пренебречь, то по аналогии с уравнением (89), составленным для стационарного режима последовательной цепи /_тг, для любого момента времени переходного режима в этой цепи можно записать:

Дифференцированием (112) по времени находим:

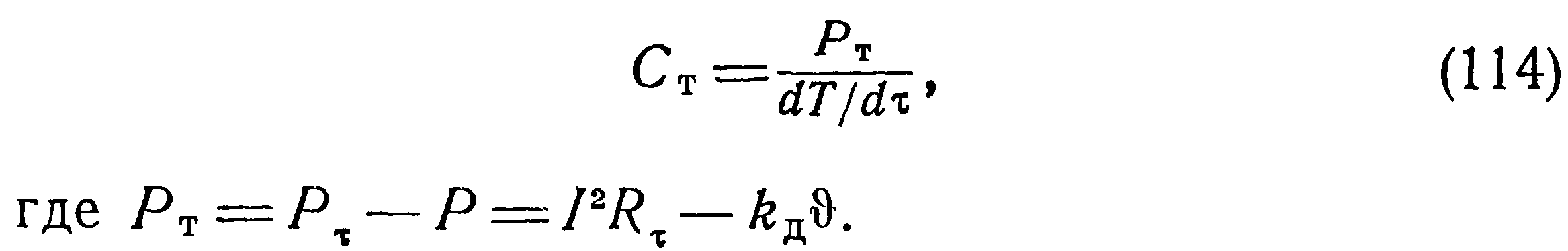
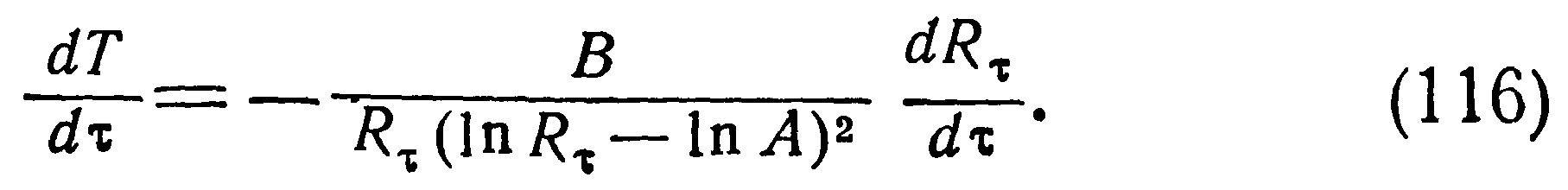
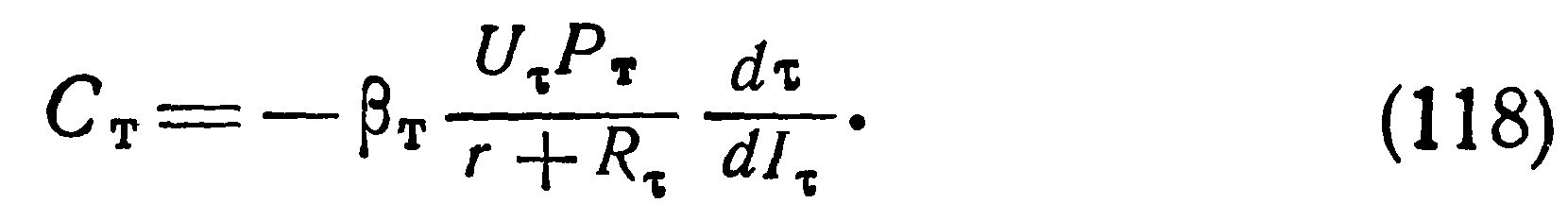
Последнее соотношение указывает на возможность использования осциллограмм тока терморезистора для расчета мгновенных значений приложенного к нему напряжения. Возможна также и обратная операция. Практическое осуществление этих возможностей облегчает обработку эксперимента, поскольку для получения расчетных параметров можно использовать осциллограммы и тока, и напряжения в зависимости от того, на каком участке переходного процесса их масштаб оказывается более удобным.

Аналитически теплоемкость терморезистора С_т может быть выражена из уравнения (108):

В полученную формулу для определения теплоемкости входят величины, которые можно получить непосредственно из статических вольт-амперных характеристик терморезистора и осциллограмм процесса его нагревания (для схемы на рис. 14 процесс г_х—>г₂). В выражение (118) вместо г нужно подставить г^э).

И окончательно с учетом полученных выше соотношений вместо (119) можно записать:

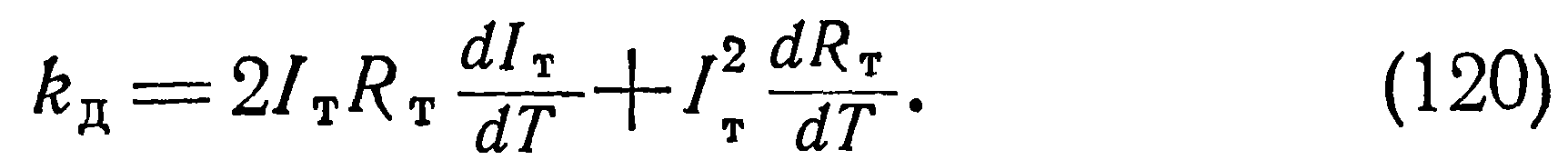
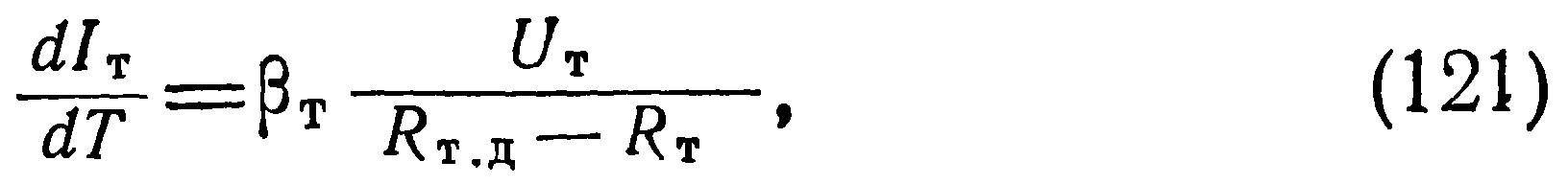
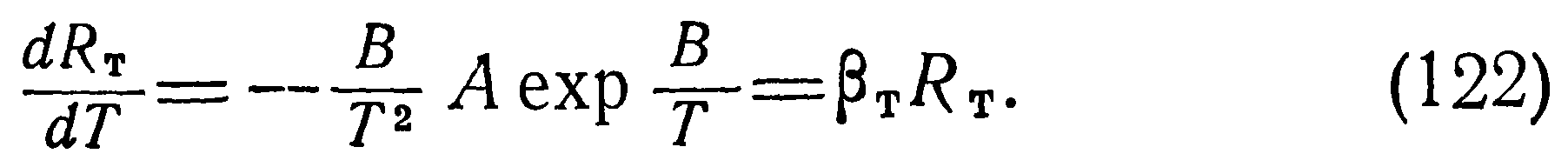
Значение тепловой постоянной времени можно вычислить как отношение по известным из формул (118) и (123) теплоемкости и динамического коэффициента рассеяния:

Постоянная времени т₀ может быть определена непосредственно из осциллограммы падения напряжения на терморезисторе в процессе его свободного охлаждения (г³₂ —*г³). При соответствующем выборе параметров схемы (рис. 14) можно получить осциллограмму напряжения на терморезисторе, когда мощность его рассеяния практически равна нулю и вторым слагаемым правой части уравнения (109) можно пренебречь. В этом случае это уравнение принимает вид:

Полученные формулы для определения объемной теплоемкости, динамической постоянной рассеяния и постоянной времени позволяют непосредственно, не прибегая к промежуточным построениям, вычислить их величину по данным статических характеристик терморезистора и осциллограмм неустановившегося процесса.

На рис. 16 приведены осциллограммы переходных процессов в цепи /_тг с терморезистором типа КМТ-11 № 2. Осциллографирование проведено в процессе нагрева и охлаждения терморезистора при постоянной температуре окружающей среды 0 =293,2° К и давлениях: атмобферном, 133 и 0,133 нм². Максимальное значение тока в установившемся режиме при атмосферном давлении выбрано 10 ма, а при давлениях, отличных от атмосферного, величина установившегося значения тока в цепи выбиралась из расчета равенства сопротивлений терморезистора при всех давлениях. Аналогичные осциллограммы были получены и для термистора типа КМТ-1 № 3.

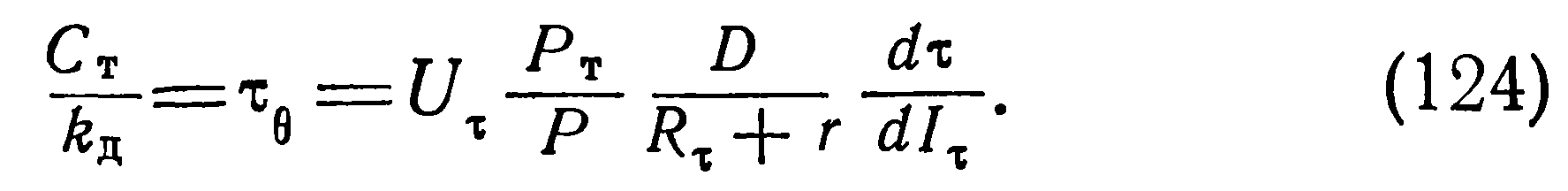
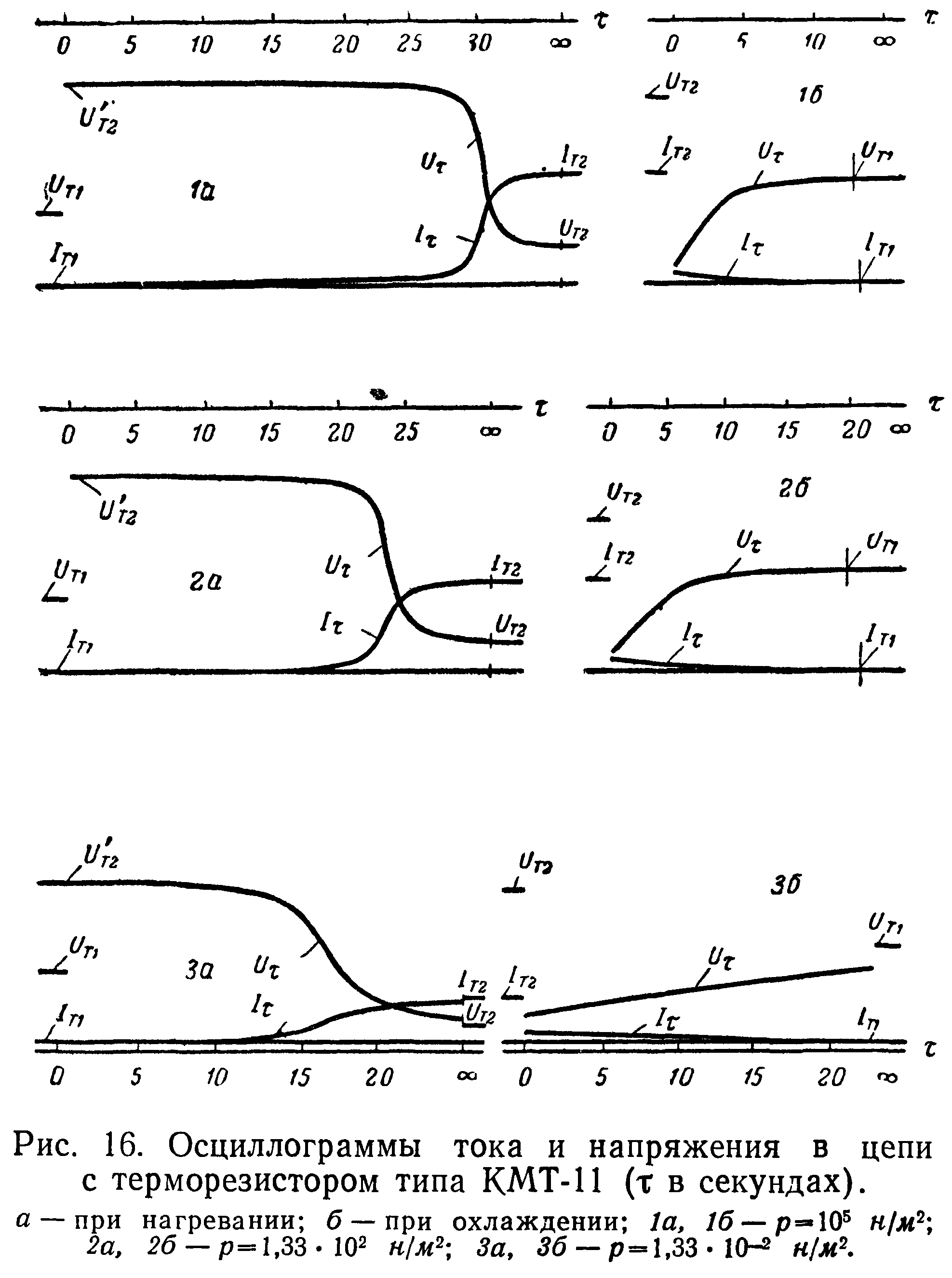
Таблица 2

Динамические параметры терморезисторов, вычисленные из их характеристик при 0 = 293, 2° К и различных давлениях

Тип и номер терморезистора	Параметры среды и терморезистора
	Р, Н/м»	о	Лд-10® emlzpad	сз Ч л* О & и	Тд сек	сек
KMT-1 КзЗ	105	1,43	2,74	101,0	36,9	46,7
	133,0	1,75	1,69	104,8	62,0	87,5
	133-10-2	1,35	0,69	110,1	160,0	229,0
КМТ-11 №2	105	3,12	0,62	2.14	3,45	4,2
	133,0	2,91	0,42	2,2	5,23	7,5
	1,33-10-2	2,52	0,1	3,1	31,0	36,9

D—динамический множитель.

Результаты обработки эксперимента сведены в табл. 2, которые получены в основном из статических вольт-амперных характеристик термисторов и осциллограмм их нагрева электрическим током при значениях исходных параметров, соответствующих точке перегиба функции S_х = /(т). Исключением являются данные для т*_в, полученные из осциллограмм процесса охлаждения терморезисторов.