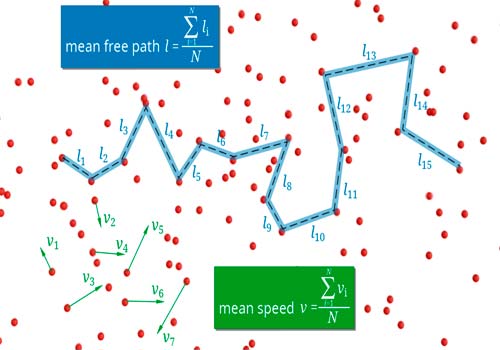
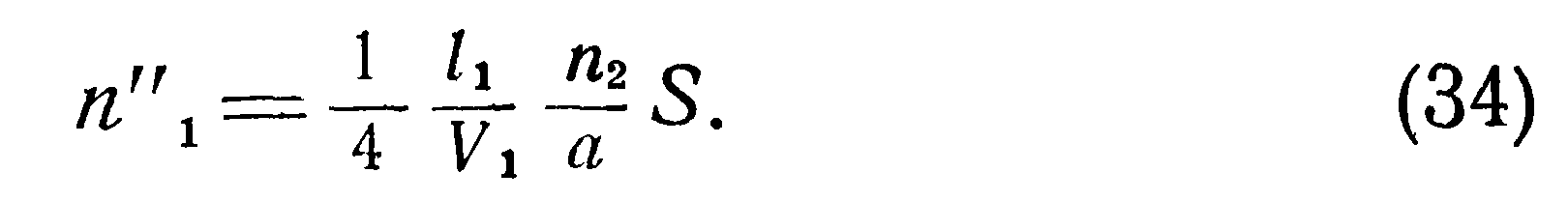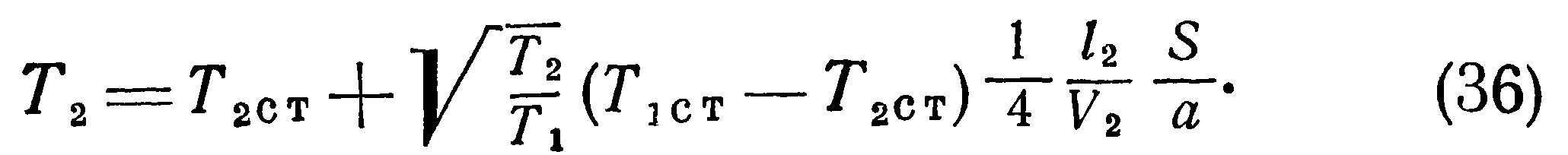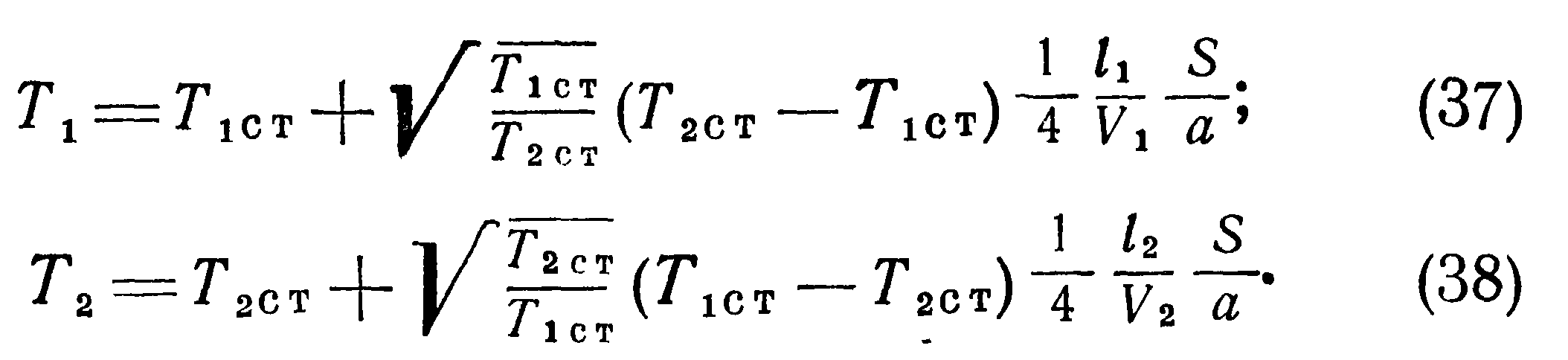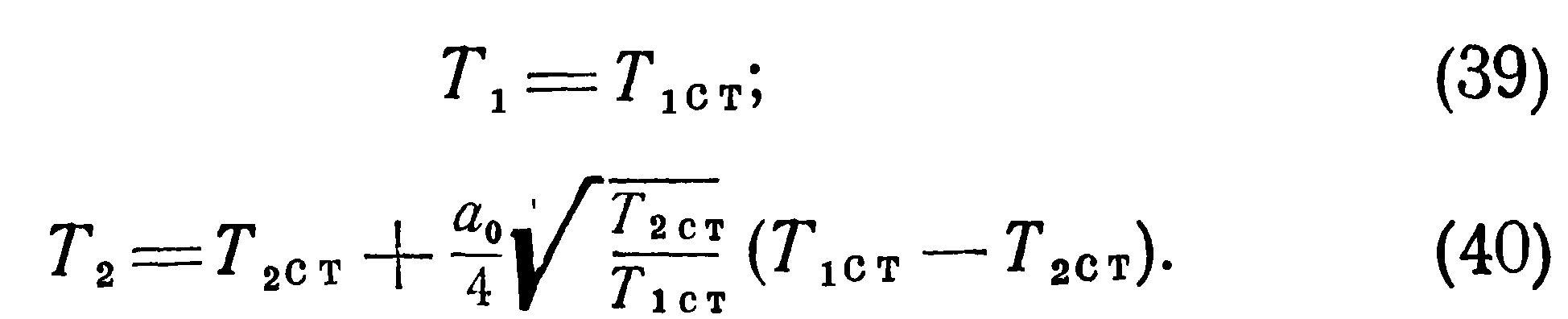Термическая эффузия газов (термомолекулярное течение)

Рассмотрим сначала течение газа через отверстие сечением S в тонкой стенке. Пусть перегородка в виде тонкой стенки отделяет два объема А и В, давление в которых соответственно р и р₂. Принимая во внимание формулу (16), выразим массу молекул, ударяющихся в единицу времени о воображаемую поверхность S, равную площади сечения отверстия.

Учитывая действительное распределение скоростей в соответствии с законом Максвелла— Больцмана и принимая во внимание соотношение (10), получим окончательно:

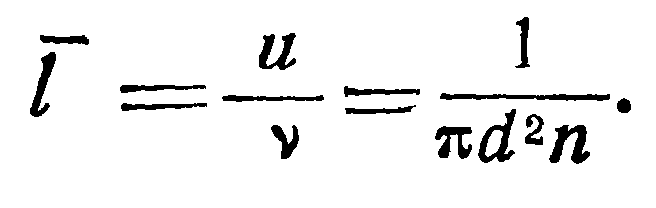
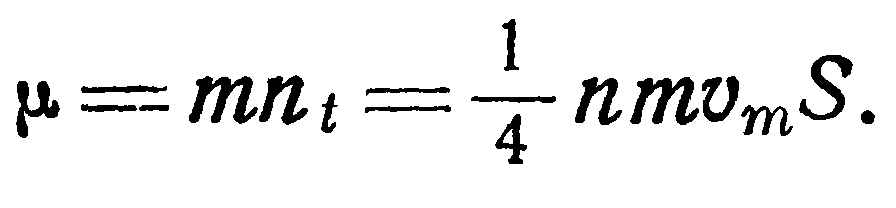
Движение молекул через отверстие происходит в обоих направлениях, но если р₂<Рь то от Л к В проходит большее число молекул. Поэтому результирующий расход газа через отверстие в единицу времени будет

При выводе этой формулы, называемой законом Грехема, предполагалось, что длина свободного пробега I намного больше диаметра отверстия.

Предположим теперь, что сосуды А и В соединены между собой тонкой трубкой, диаметр которой мал по сравнению с длиной свободного пробега. Пусть давления в обоих сосудах вначале одинаковы (pi=p₂), а температуры различны, например Ti>T₂. Тогда условие равновесия выразится равенством проходящего по трубке в единицу времени количества молекул в обоих направлениях.

При отсутствии разности температур между сосудами концентрация молекул в них одинакова и будет равна n = N/(Vi + V₂), где N — полное число молекул в обоих сосудах. При возникновении разности температур между ними для выполнения условия равновесия (19) должно иметь место одностороннее перемещение частиц из сосуда с более высокой температурой в сосуд с более низкой температурой.

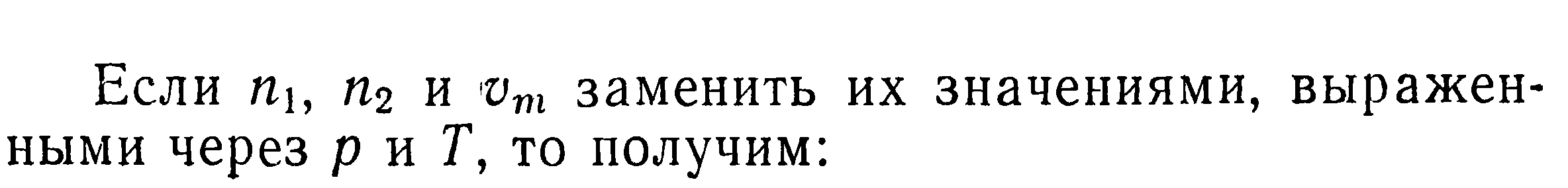
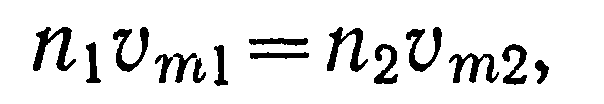
Из уравнения (10) с учетом полученных выше соотношений находим:

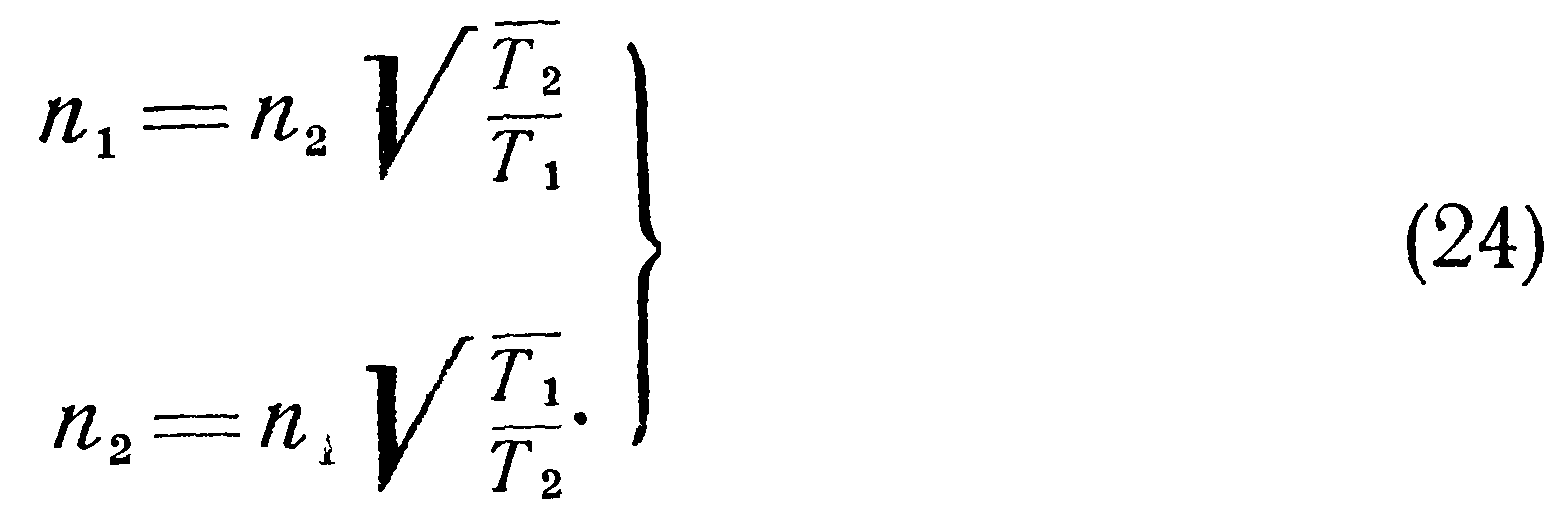
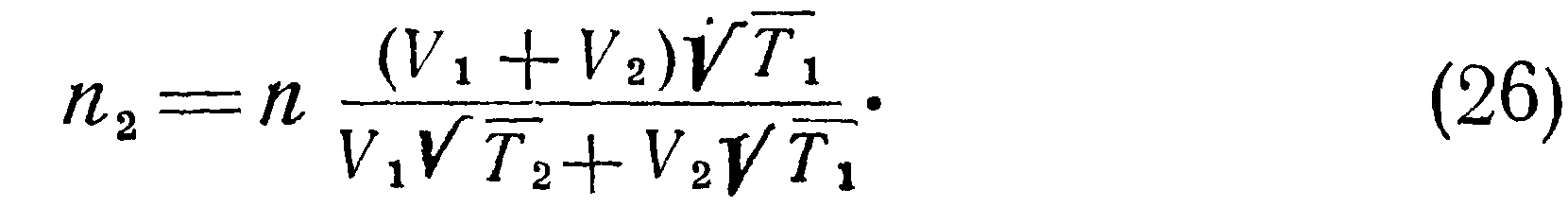
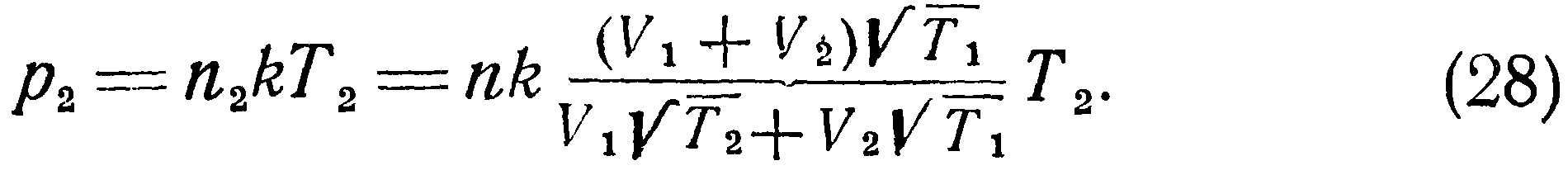
В этом случае будут справедливы соотношения:

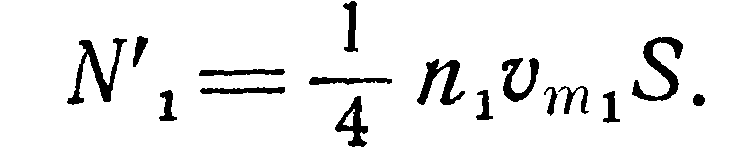
До столкновения с молекулами второго сосуда, средняя скорость которых равна или с его стенкой, N молекул будут обладать скоростью При столкновениях N молекул приобретают скорость, близкую к v_m2 и отличающуюся от v_m2 в а раз, где а — коэффициент аккомодации, который характеризует степень обмена энергией молекул газа и твердой стенки.

Полное число молекул во втором сосуде, обладающих скоростью v_m, будет,где 1₂— величина, равная длине свободного пробега Z, зависящей от температуры и давления.

Число молекул проходящее в единицу времени через поперечное сечение 5 соединительной трубки из первого сосуда во второй со скоростью v_m, может быть выражено формулой:

>Полученные выше соотношения указывают на наличие особенностей температурного режима разреженного газа, заключенного в двух сообщающихся сосудах с различными температурами стенок. Эти особенности, вызванные молекулярной структурой газа, необходимо учитывать при конструировании датчиков давления. Формулы (25) — (40) позволяют вычислять действительные температуры, давления и плотности находящегося в сообщающихся сосудах сильно разреженного газа. Однако их вывод сделан для условий свободного молекулярного течения в предположении, что длина трубки мала по сравнению с длиной свободного пробега I и оба конца трубки имеют температуру соответственно Тют и Тзст. Поэтому для реальных условий эти формулы дают лишь качественную картину явления и, как будет ниже показано экспериментально, с повышением давления влияние отмеченных особенностей не проявляется.