Основы кинетической теории газов

Для газообразного состояния вещества характерна большая подвижность молекул, вследствие чего газ не имеет определенного объема и формы, а занимает весь объем и принимает форму сосуда, в котором он находится.

Важнейшими термодинамическими параметрами (признаками) газа являются его температура и давление. Оба эти параметра могут характеризовать лишь массу вещества, состоящего из большого числа частиц, и теряют смысл по отношению к одной элементарной, частице (атому, молекуле или электрону).

В физике и технике давление измеряется в единицах силы, приходящейся на единицу площади. Наиболее употребительными единицами являются: миллиметр ртутного столба (мм рт. ст.), физическая атмосфера (1 ат=760 мм рт. ст.) и единица давления в международной системе единиц СИ (1 н/м² = 7,5006 • 10-³ ммрт. ст. и, следовательно, 1 мм рт. ст. = 133,322 нм²).

Физические свойства разреженного газа связаны со степенью его разрежения, которая существенно влияет на характер течения газа и его взаимодействие с твердой стенкой. Основным критерием, характеризующим степень разрежения газа, является критерий Кнудсена:

Для описания физических процессов, происходящих в вязком потоке газа, пользуются обычными законами газовой динамики. Процессы, происходящие при течениях газа в молекулярно-вязкостном и молекулярном режимах, намного сложнее и вызывают необходимость учитывать дискретность структуры газа на основе кинетической теории газов. С точки зрения этой теории газ состоит из отдельных молекул, непрерывно и хаотически двигающихся в пространстве. Молекулы взаимодействуют друг с другом только при соударениях и их траектории представляют собой ломаные линии.

При рассмотрении находящегося в сосуде газа необходимо иметь в виду, что молекулы газа сталкиваются не только друг с другом, но и со стенками сосуда. Удары молекул о стенки сосуда воспринимаются ею как давление р. В промежутках между столкновениями каждая молекула движется с некоторой скоростью, соответствующей ее кинетической энергии. После каждого столкновения скорость молекул изменяется как по величине, так и по направлению. В общей массе газа кинетическая энергия движущихся молекул является мерой его тепловой энергии, а среднестатическое перемещение всех молекул характеризуется температурой газа. Таким образом, абсолютная температура газа пропорциональна средней кинетической энергии движения всех молекул.

Одним из основных допущений кинетической теории является то, что газ является средой изотропной, т. е. в ней нет каких-либо преимущественных направлений.

При выводе количественных соотношений, выражающих давление идеального газа, принимается, что удар молекулы массой т о стенку идеально упругий.

В этом случае скорость ударившейся молекулы меняется на устанавливающий связь между длиной свободного пробега 1 (расстоянием, пробегаемом молекулой газа без соударения с другой молекулой) и характерным размером системы d.

Отсюда давление, оказываемое одной молекулой на стенку площадью 5, можно выразить в виде и тогда давление, оказываемое молекулами числом n_t, будет:

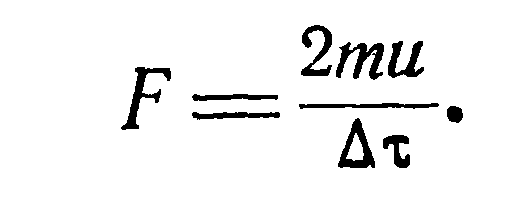
Учитывая последнее, окончательно получим:

Аналогичное соотношение получим для средней скорости с любого направления. Пусть u, v, w — три компоненты скорости с, тогда можно написать u² + v² + w² = = с², а вследствие изотропности среды.

Замечаем далее, что произведение пт является плотностью газа р и, следовательно,

Подставляя (3) в (2), получим:

и—(—u)=2u, а средняя сила ее удара за время Ат будет:

Для грамм-молекулы массой М и объемом V плотность запишется в виде

Тогда формула (7) перепишется:

откуда

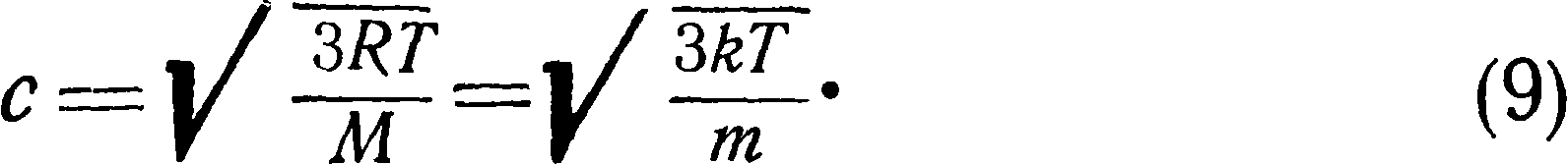
Число молекул п, заключающееся в единице объема, можег быть получено из формулы (4):

а с учетом соотношения (9) получим окончательно:

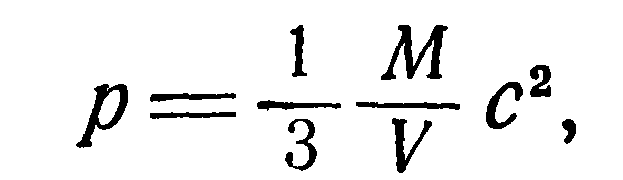
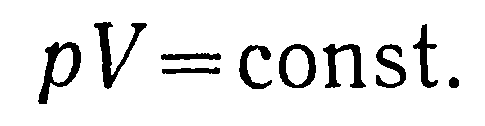
где R — универсальная газовая постоянная;

Т — абсолютная температура газа.

При неизменной температуре газа Т произведение давления р на объем V будет постоянной величиной, что выражает собой закон Бойля — Мариотта:

Из формулы (8) можно вычислить среднюю квадратичную скорость молекул газа, что свидетельствует о независимости концентрации молекул от природы газа.

Из полученных выше зависимостей вытекает формула Менделеева — Клапейрона:

устанавливающая связь между плотностью газа, его давлением и температурой.

Одним из фундаментальных положений кинетической теории газов является представление о распределении скоростей молекул. Вследствие непрерывных соударений молекул газа их скорости непрерывно меняются. Однако благодаря тому, что число молекул даже при очень низких давлениях велико, можно принять, что в любой момент число молекул, имеющих определенные скорости по величине и по направлению, сохраняется одинаковым. В следующий момент эти молекулы меняют свои скорости, но зато другие приобретают такие же. Иначе говоря, существует устойчивое распределение скоростей, количественно выражающееся функцией распределения Максвелла—Больцмана:

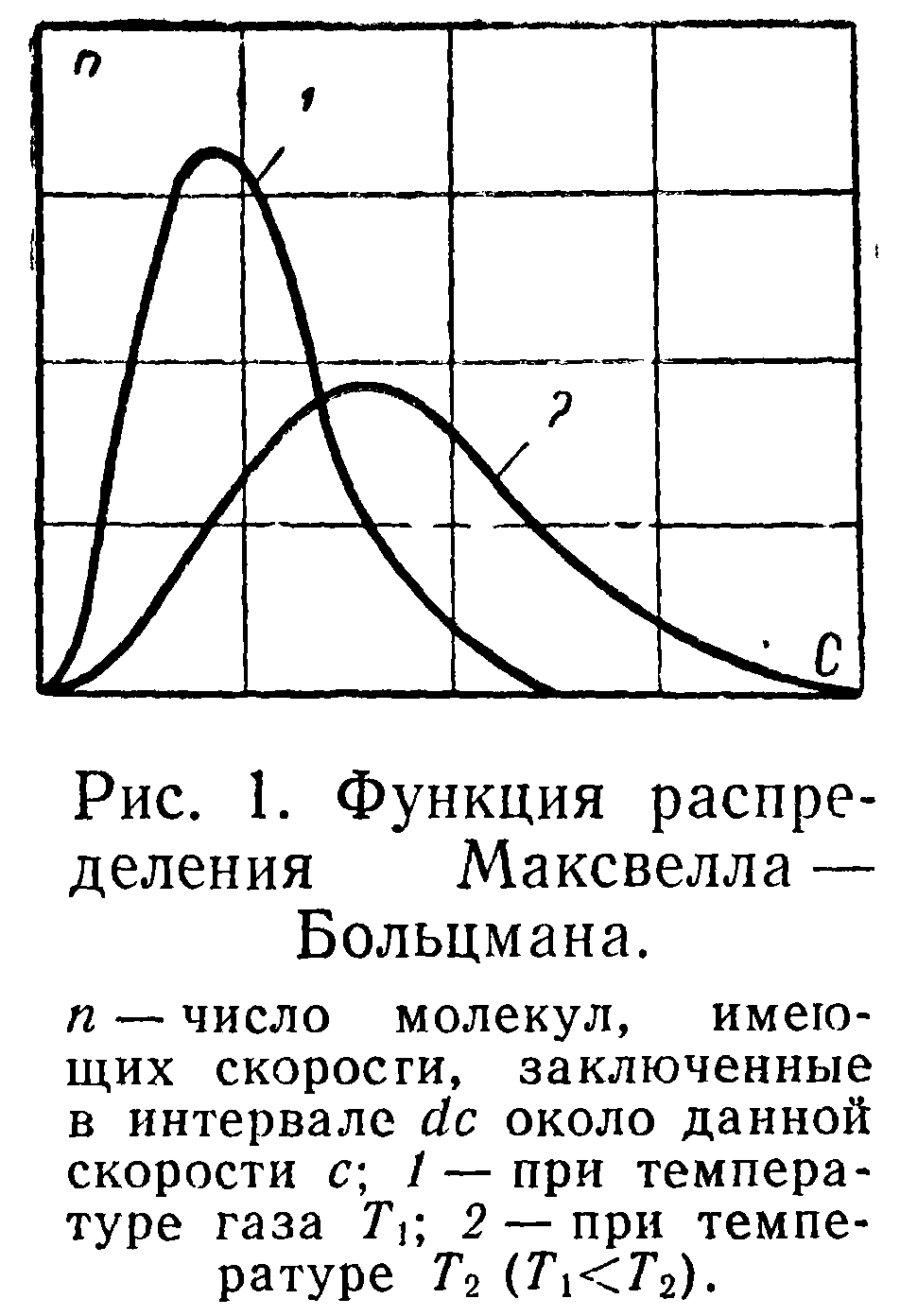
На рис. 1 изображены кривые для функции распределения dnldc-f(c), которые соответствуют двум различным абсолютным температурам, взятым как параметры.

Зная функцию распределения, можно определить величину наиболее вероятной скорости v_p (скорость, с которой движется наибольшее число молекул в данный момент). Значение v_p получим, приравняв нулю производную от функции распределения:

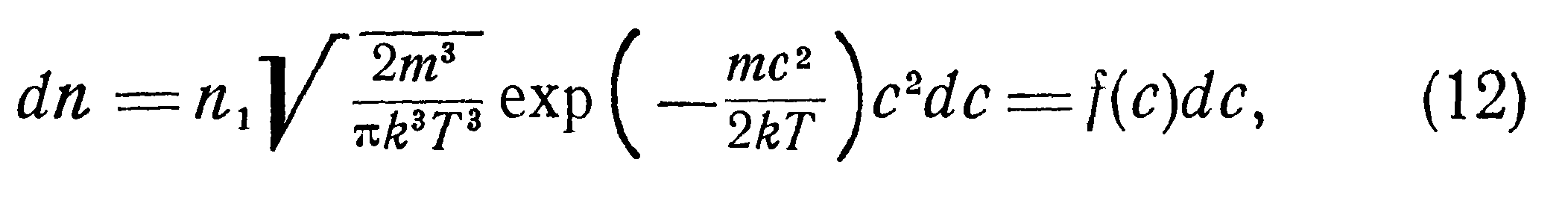
Сопоставляя формулы (9) и (14), получим соотношение между среднеквадратичной и среднеарифметической скоростями:

При более строгом выводе — если учесть, что молекулы ударяются о стенки под различными углами и не все скорости направлены нормально к стенке, то коэффициент л/2 следует заменить единицей. В этом случае получим:

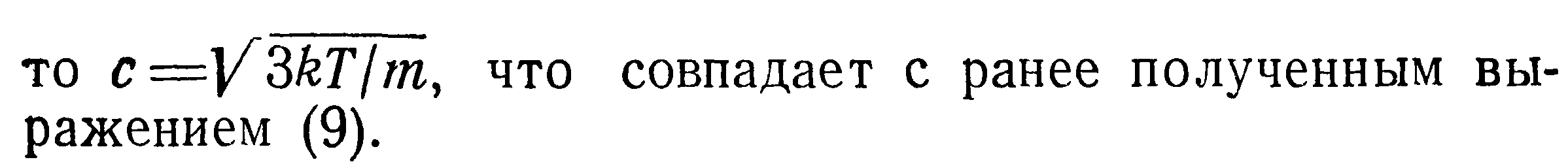
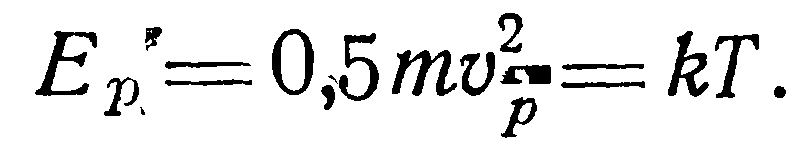
Скорость, которая получается в результате суммирования большого числа скоростей молекул и деления этой суммы на число молекул, является средней арифметической.

Скорость, соответствующая средней кинетической энергии молекулы, является средней квадратичной скоростью с.

Так как:

Для вывода формулы средней длины свободного пробега предположим, что диаметр молекулы равен d. Заметим далее, что две молекулы в процессе хаотического движения могут столкнуться между собой лишь в том случае, если их центры пройдут на расстоянии друг от друга не больше d. Для простоты рассуждений можно принять, что рассматриваемая молекула имеет диаметр, равный 2d, а остальные молекулы являются просто точками.

Если скорость молекулы диаметром 2d равна и, то в единицу времени она опишет объем, равный Ttd²u. При молекулярной концентрации п этим объемом будет задето число центров остальных молекул, равное v = = nd² ит, что будет равно числу столкновений в единицу времени. Отсюда, предполагая скорости всех молекул одинаковыми, получим выражение для средней длины свободного пробега.