Влияние побочных явлений на чувствительность и статическую точность датчика

Для характеристики результата преобразования или измерения обычно употребляется термин «точность преобразования (измерения)», обозначающий степень приближения преобразования к действительному значению преобразуемой величины. Количественно оценка результата преобразования (измерения) определяется погрешностью датчика или прибора. Погрешность может быть абсолютной, выраженной в единицах преобразуемой величины, и относительной, которая выражается в процентах от ее действительного значения.

По природе возникновения погрешности делятся на систематические (погрешности установки, инструментальные, методические) и случайные. Здесь будут рассматриваться только методические погрешности, т. е. те, которые являются следствием упрощающих предпосылок при выводе количественных соотношений между входными и выходными параметрами датчика. Другие виды погрешностей не являются в данном случае специфичными и не представляют поэтому практического интереса.

В связи с этим важно проанализировать причины, могущие вызвать методическую погрешность преобразования выходной величины датчика и рассмотреть влияние побочных явлений на его чувствительность. Под побочными явлениями здесь подразумеваются явления, которые не учитывались при выводе статических характеристик и чувствительности датчика и его отдельных звеньев, т. е. потери тепла лучеиспусканием и по подводящим проводам. Кроме того, наличие температурных градиентов в теле датчика тоже приводит к увеличению его погрешности.

При выводе формул для чувствительности датчика предполагалось, что вся теряемая им мощность происходит за счет совместного действия конвекции и теплопроводности с поверхности самого датчика. Предварительно проведенные расчеты теплообмена терморезисторов и экспериментальные данные свидетельствуют о том, что для стандартных терморезисторов потери тепла через подводящие провода и излучением с поверхности самих рабочих тел в диапазоне их рабочих температур составляют порядка 50% полных потерь и более. При этом потери на излучение резко возрастают по мере увеличения температуры. Если теперь учесть, что в соответствии с формулами (151), (155) чувствительность обратно пропорциональна рассеиваемой мощности (или /²), то отрицательное явление побочных потерь на чувствительность датчика очевидно. Кроме того, как следует из этих формул, чувствительность датчика пропорциональна квадрату перепада температур ft² (для датчика, работающего в условиях вязкого потока, эта пропорциональность выше второй степени). Следовательно, снижение чувствительности может происходить вследствие уменьшения перепада температур за счет побочных потерь тепла.

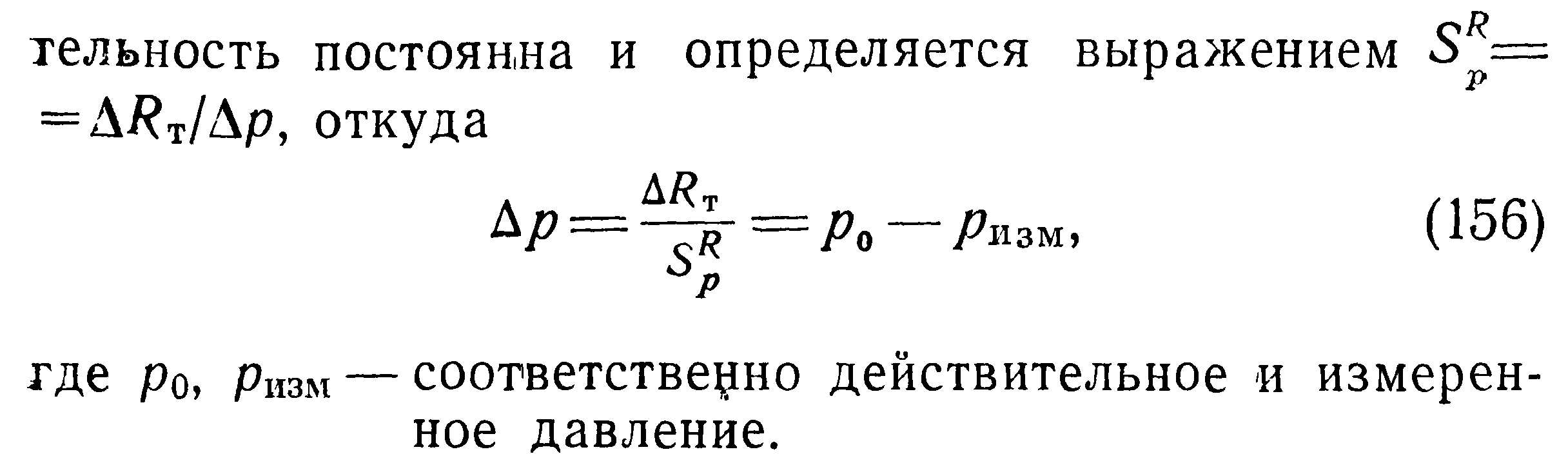
Следует также учитывать и другую сторону влияния подводящих проводов на чувствительность датчика. Механизм потерь по подводящим проводам характеризуется тем, что при распространении тепла под действием перепада температур между горячим концом провода и холодным происходит одновременное его рассеяние в окружающую среду. Таким образом, величина потерь по проводам является функцией коэффициента теплообмена ia_n между проводом и средой, зависящего в свою очередь от его геометрических размеров (в данном случае диаметра). Вследствие того, что определяющие размеры проводов и тела самого датчика, вообще говоря, -различны, то при одном и том же давлении их теплообмен со средой может происходить по различным законам и иметь существенные количественные различия. -Следовательно, чувствительность датчика является функцией этих двух совместно протекающих процессов. Именно поэтому зависимость a = (p(lgp) на рис. 22 более плавная (и не имеет производных, равных нулю) по сравнению с зависимостью aK=<Pi(lg р).

Соответствующий подбор геометрических размеров и физических свойств системы «датчик — подводящий провод» может повысить чувствительность датчика в целом. Очевидно, подводящие провода должны быть очень тонкими. Из этих же соображений датчик целесообразно снабжать тонкими ребрами в виде пластин и пленок.

Основной причиной возникновения погрешности во втором звене является влияние изменения температуры окружающей среды. О мерах, предпринимаемых для снижения погрешности по указанной причине, речь будет идти ниже. Здесь следует остановиться на определении погрешности измерения О, возникающей вследствие наличия градиентов температуры в теле датчика. С этой целью предпринято исследование температурного поля в теле терморезистора, сводящееся к решению уравнения теплопроводности и его анализу.

Используя интегральную характеристику терморезистора, его среднеобъемную температуру Т как независимый параметр, уравнение теплопроводности для терморезистора как для цилиндра бесконечной длины решена при следующих дополнительных условиях:

1) источники тепла равномерно распределены па объему терморезистора и коэффициент теплопроводности X — величина постоянная; 2) распределение источников тепла является функцией температуры и физических констант материала терморезистора, Z = const; 3) источники равномерно распределены по объему, а коэффициент теплопроводности линейно зависит от температуры.

1. В первом случае (Х = const) уравнение теплопроводности для стационарного режима будет иметь вид:

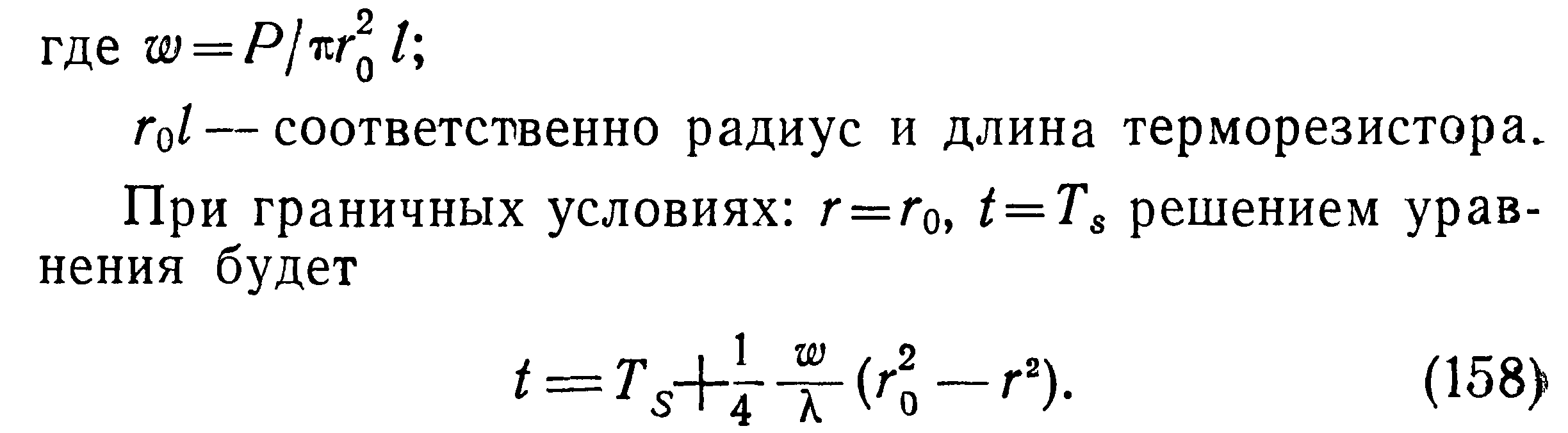
Температуру поверхности для цилиндрического терморезистора T_s удобно выразить через среднеобъемную температуру Т, для чего запишем:

После подстановки в уравнение (159) значения /(г) мз уравнения (158) и его решения относительно T_s получим:

Последующая подстановка (159) в уравнение (160) дает решение в окончательном виде

2. Распределение источников — функция температуры .и физических констант терморезистора, X=const.

Для терморезисторов, удельное электрическое сопротивление которых имеет зависимость от температуры вида (76), удельное объемное тепловыделение может стать в значительной степени неравномерным вследствие неодинаковой температуры по сечению.

Уравнение теплопроводности для этого случая запишется в виде, решением которого будет:

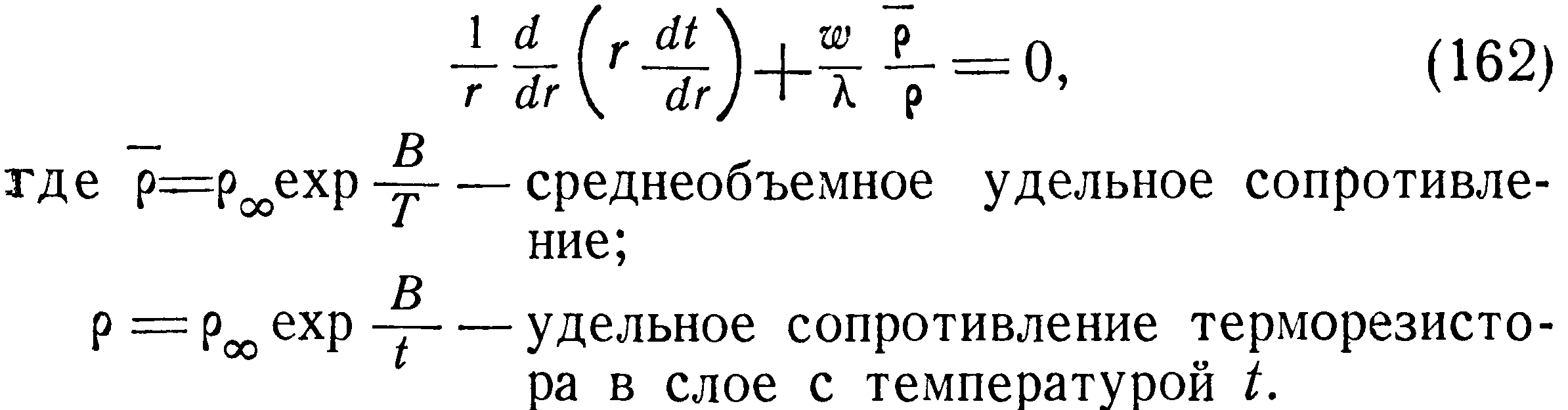
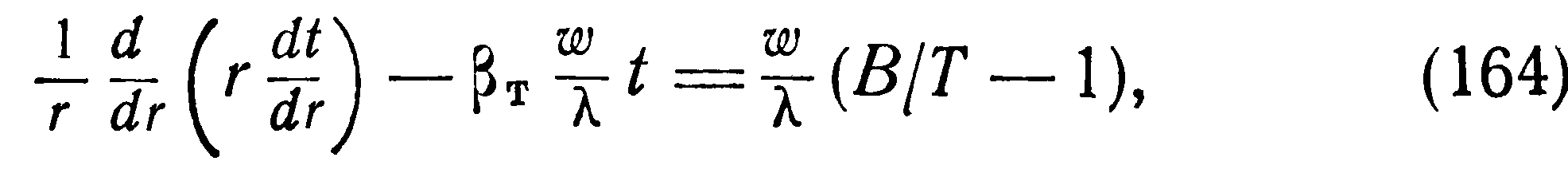
Разлагая отношение удельных сопротивлений р/р в ряд Тейлора и ограничиваясь для случая небольших перепадов температур линейными членами ряда, получим:

С учетом (163) после преобразований уравнение (162) примет вид:

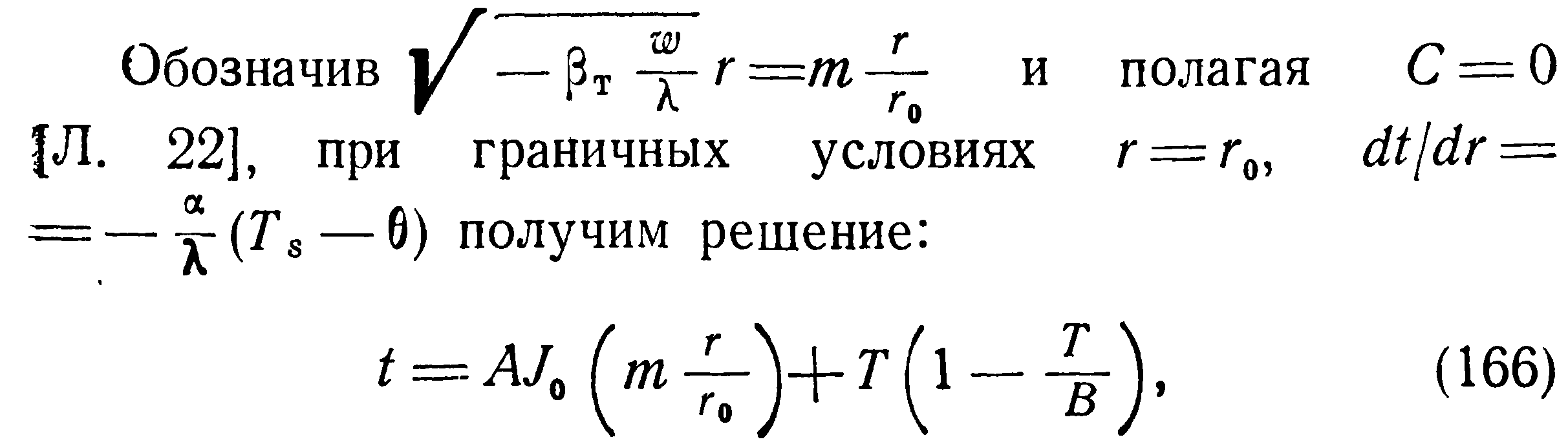
где

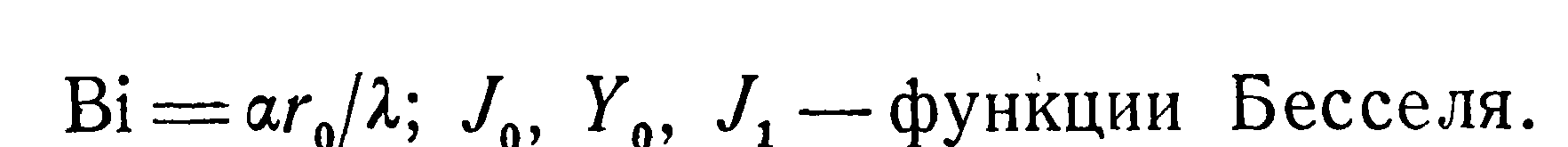
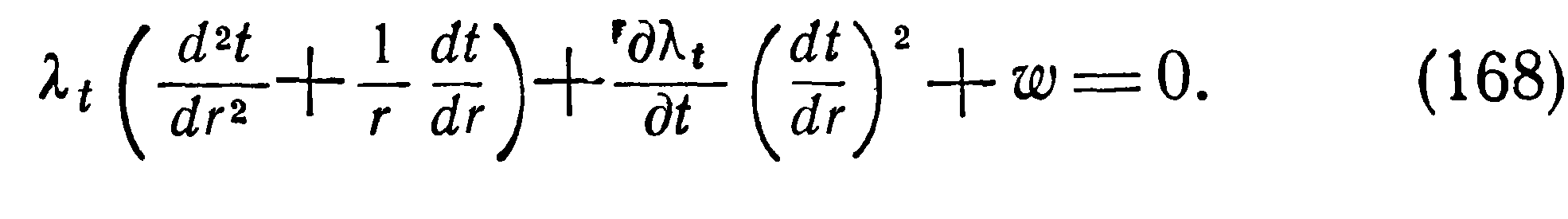
3. Источники тепла равномерно распределены по объему, коэффициент теплопроводности.

Уравнение теплопроводности запишется:

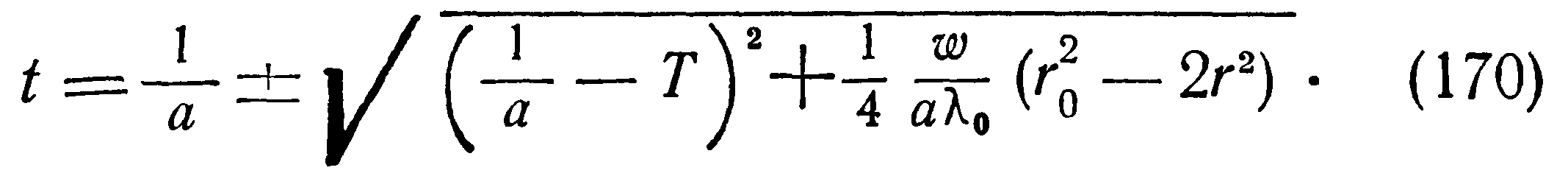
Для получения реальных значений температур знак перед корнем в выражении (170) выбирается в зависимости от знака коэффициента а: при положительном а — знак плюс, при отрицательном — знак минус.

Проведенные расчеты и анализ показывают, что влияние неравномерности объемного тепловыделения на величину градиента температуры незначительно и его действие находится за пределами точности измерения среднеобъемной температуры. Если к тому учесть, что действие этого эффекта противоположно по знаку действию эффекта температурной зависимости X при а>0, то становится очевидным, что для практических расчетов температуры внутри терморезисторного датчика и на его поверхности можно ограничиться простейшими формулами (160) и (161). Точность расчетов в этом случае будет определяться точностью измерения среднеобъемной температуры Т.

Для оценки величин градиента температуры в теле терморезисторов типа КМТ-1 и КМТ-11 проведены расчеты температуры их поверхности по формуле (160). Значение коэфициента теплопроводности принято по данным Г. Н. Дульнева для кобальтово-марган-цевой смеси (материала терморезисторов типа КМТ). В зависимости от процентного содержания марганца и температуры коэффициент теплопроводности изменяется в пределах от 1,8 до 3,8 вт/мград (здесь использовано нижнее значение этого коэффициента). Расчет выполнен по данным характеристик образцов КМТ-1 № 3 и КТМ-11 № 2, снятых в условиях атмосферного давления и в вакууме (р <10^-2 я/ж²) при температуре среды 6 = = 293,2° К. Для сопоставимости расчетов координаты вольт-амперных характеристик взяты при неизменной среднеобъемной температуре 7=358 и 467° К соответственно для терморезисторов типа КМТ-1 и КМТ-11. В результате расчетов получено: а) для КМТ-1 в атмосфере Д7=7—7_s = 0,46°, в вакууме Д7=0,11°; б) для КМТ-11 в атмосфере Д7=1,63°, в вакууме Д7=0,24°. Вычисленная по формуле (181) (см. ниже) в соответствии с этими данными погрешность датчика не превышает 2%. Последнее свидетельствует о пренебрежимо малом влиянии градиента температуры в теле теплоэлектрического датчика давления на его чувствительность и статическую точность.

Устройство и принцип работы терморезисторов с металлическими контактными колпачками дают основание предполагать, что при прохождении по терморезистору электрического тока возможно появление трех основных термоэлектрических эффектов: Пельтье, Зеебека, Томсона.

Для качественной оценки влияния эффекта Пельтье на распределение температуры в теле терморезистора типа КМТ-1 № 2 проведено экспериментальное измерение температуры при помощи медь-константановых термопар в месте перехода от рабочей части терморезистора к контактным колпачкам. Измерительная схема позволяла регулировать ток от 0 до 50 ма, мгновенно изменять его направление и фиксировать изменение температуры в месте контакта. Измерения показали, что величина градиента температуры в осевом направлении терморезистора лежит за пределами точности измерения температуры при помощи термопар.

Таким образом, влиянием эффекта Пельтье, а следовательно, и эффектами Зеебека и Томсона на распределение температуры по поверхности кобальтово-марганцевых термисторов можно пренебречь.

Справедливость сделанных выводов вытекает из проведенных измерений падения напряжения по образующей цилиндра рабочей части терморезистора типа КМТ-1 № 2 (рис. 24). Напряжение измерялось ламповым вольтметром при четырех различных значениях тока термистора по схеме, изображенной на рис. 24. Для съема напряжения использовался зонд с микрометрической подачей и отсчетом через 0,1 мм.

Линейная зависимость падения напряжения от координаты по длине образующей свидетельствует о равномерном разогреве терморезистора по длине его рабочей части, а резкие скачки напряжения в месте соединения с контактными колпачками — о большой величине утечки тепла с торцов. Проверено, что при перемене направления тока абсолютная величина скачков напряжения не изменяется.